
【题目】设函数![]() 的定义域为
的定义域为![]() ,值域为
,值域为![]() ,如果存在函数
,如果存在函数![]() ,使得函数
,使得函数![]() 的值域仍是
的值域仍是![]() ,那么称
,那么称![]() 是函数
是函数![]() 的一个等值域变换.
的一个等值域变换.
(1)判断下列函数![]() 是不是函数
是不是函数![]() 的一个等值域变换?说明你的理由;
的一个等值域变换?说明你的理由;
①![]() ;
;
②![]() .
.
(2)设![]() 的定义域为
的定义域为![]() ,已知
,已知![]() 是
是![]() 的一个等值域变换,且函数
的一个等值域变换,且函数![]() 的定义域为
的定义域为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1)①不是等值域变换,②是等值域变换; (2)![]() .
.
【解析】试题分析:(1)运用对数函数的值域和基本不等式,结合新定义即可判断①;运用二次函数的值域和指数函数的值域,结合新定义即可判断②;
(2)利用f(x)的定义域,求得值域,根据x的表达式,和t值域建立不等式,利用存在t1,t2∈R使两个等号分别成立,求得m和n.
试题解析:
(1)①![]() ,x>0,值域为R,
,x>0,值域为R,
![]() ,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
,t>0,由g(t)2可得y=f[g(t)]的值域为[1,+∞).
则x=g(t)不是函数y=f(x)的一个等值域变换;
②![]() ,即
,即![]() 的值域为
的值域为![]() ,
,
当![]() 时,
时, ![]() ,即
,即![]() 的值域仍为
的值域仍为![]() ,所以
,所以![]() 是
是![]() 的一个等值域变换,故①不是等值域变换,②是等值域变换;
的一个等值域变换,故①不是等值域变换,②是等值域变换;
(2)![]() 定义域为
定义域为![]() ,因为
,因为![]() 是
是![]() 的一个等值域变换,且函数
的一个等值域变换,且函数![]() 的定义域为
的定义域为![]() ,
, ![]() 的值域为
的值域为![]() ,
,
![]() ,
,
![]() 恒有
恒有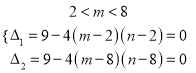 ,解得
,解得 .
.


科目:高中数学 来源: 题型:
【题目】如图, ![]() 是
是![]() 直径,
直径, ![]() 所在的平面,
所在的平面, ![]() 是圆周上不同于
是圆周上不同于![]() 的动点.
的动点.
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且当二面角
,且当二面角![]() 的正切值为
的正切值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱![]() 中,底面
中,底面![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 分别为线段
分别为线段![]() ,
, ![]() 的中点.
的中点.
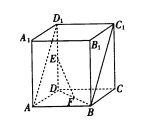
(1)求证: ![]() ||平面
||平面![]() ;
;
(2)四棱柱![]() 的外接球的表面积为
的外接球的表面积为![]() ,求异面直线
,求异面直线![]() 与
与![]() 所成的角的大小.
所成的角的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系内,已知![]() 是圆
是圆![]() 上一点,折叠该圆两次使点
上一点,折叠该圆两次使点![]() 分别与圆上不相同的两点(异于点
分别与圆上不相同的两点(异于点![]() )重合,两次的折痕方程分别为
)重合,两次的折痕方程分别为![]() 和
和![]() ,若圆
,若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,其中
,其中![]() 的坐标分别为
的坐标分别为![]() ,则实数
,则实数![]() 的取值集合为__________.
的取值集合为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元?
(2)当一次订购量为![]() 个, 每件商品的实际批发价为
个, 每件商品的实际批发价为![]() 元,写出函数
元,写出函数![]() 的表达式;
的表达式;
(3)根据市场调查发现,经销商一次最大定购量为![]() 个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于定义域分别是A,B的函数![]() ,
, ![]() ,规定:
,规定: 
现给定函数![]()
(1) 若![]() ,写出函数
,写出函数![]() 的解析式;
的解析式;
(2) 当![]() 时,求问题(1)中函数
时,求问题(1)中函数![]() 的值域;
的值域;
(3) 请设计一个函数![]() ,使得函数
,使得函数![]() 为偶函数且不是常数函数,并予以证明.
为偶函数且不是常数函数,并予以证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]()
![]() 在某一周期内的图象时,列表并填入了部分数据,如下表:
在某一周期内的图象时,列表并填入了部分数据,如下表:
| 0 |
|
|
|
|
|
|
| |||
| 0 | 2 | 0 | 0 |
(Ⅰ)请将上表数据补充完整,函数![]() 的解析式
的解析式![]() (直接写出结果即可)
(直接写出结果即可)
(Ⅱ)求函数![]() 的单调递增区间;/span>
的单调递增区间;/span>
(Ⅲ)求函数![]() 在区间
在区间![]() 上的最大值和最小值.
上的最大值和最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若二次函数f(x)=ax2+bx+c(a、b∈R)满足f(x+1)﹣f(x)=2x,且f(0)=1.
(1)求f(x)的解析式;
(2)若在区间[﹣1,﹣1]上,不等式f(x)>2x+m恒成立,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com