考点:三角函数中的恒等变换应用,复合三角函数的单调性
专题:计算题,三角函数的图像与性质
分析:(1)由三角函数中的恒等变换应用化简函数解析式可得f(x)=2sin(2x+
)+1,由已知可求a,由2k
π+≤2x+
≤2k
π+,k∈Z得函数f(x)的单调递减区间.
(2)由x∈[-
,
],可求-
≤2x+
≤
,解得sin(2x+
)的范围,即可求出函数f(x)的值域.
解答:
(本小题满分12分)
解:(1)∵函数f(x)=2
sinxcosx+acos
2x的图象经过点(0 2),
∴f(0)=2,
∴a=2,…(2分)
∴f(x)=
sin2x+2cos
2x=
sin2x+cos2x+1=2sin(2x+
)+1,…(6分)
∴由2k
π+≤2x+
≤2k
π+,k∈Z得k
π+≤x≤
+kπ,k∈Z,
∴函数f(x)的单调递减区间函数f(x)的单调递减区间为:[k
π+,
+kπ],k∈Z,…(8分)
(2)由(1)知f(x)=2sin(2x+
)+1,
∵x∈[-
,
],
∴-
≤2x+
≤
,
∴
-≤sin(2x+
)≤1,…(10分)
∴0≤f(x)≤3,即函数f(x)的值域为[0,3].…(12分)
点评:本题主要考查了三角函数中的恒等变换应用,复合函数的单调性,属于基本知识的考查.



 综合自测系列答案
综合自测系列答案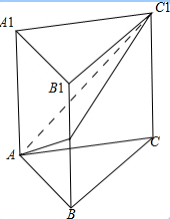 如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为
如图,直三棱柱ABC-A1B1C中,AB⊥BC,AB=4,BC=6,AA1=8,有一只蚂蚁沿着三棱柱的表面从点A爬行到点C1,并且在棱BB1上的一点M稍作停顿,当蚂蚁爬行距离最短时,BM的长度为