
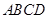 为直角梯形,
为直角梯形,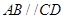 ,
,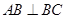 ,
,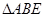 为等边三角形,且平面
为等边三角形,且平面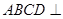 平面
平面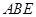 ,
,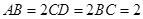 ,
,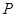 为
为 中点.
中点.
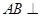
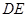 ;
;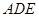 与平面
与平面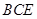 所成的锐二面角的余弦值;
所成的锐二面角的余弦值;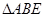 内是否存在一点
内是否存在一点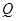 ,使
,使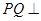 平面
平面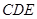 ,如果存在,求
,如果存在,求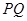 的长;如果不存在,说明理由.
的长;如果不存在,说明理由. 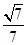 ;(3)
;(3)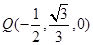 ,
,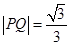
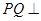 平面
平面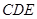 ,只需要向量PQ,与平面内任一两条直线所对应的向量的数量积为零即可,从而求出点Q的坐标即线段PQ的长.
,只需要向量PQ,与平面内任一两条直线所对应的向量的数量积为零即可,从而求出点Q的坐标即线段PQ的长.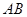 中点
中点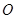 ,连结
,连结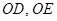 ,
,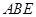 是正三角形,所以
是正三角形,所以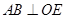 .
.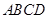 是直角梯形,
是直角梯形,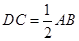 ,
,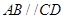 ,
,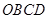 是平行四边形,
是平行四边形,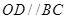 ,
,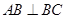 ,所以
,所以 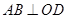 .
.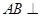 平面
平面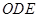 ,
,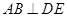 .
.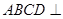 平面
平面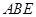 ,
,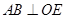 ,所以
,所以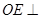 平面
平面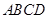 ,
,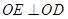 .
.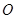 为原点建立空间直角坐标系.
为原点建立空间直角坐标系. 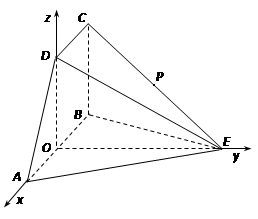
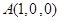 ,
,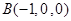 ,
,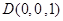 ,
,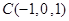 ,
,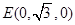 .
.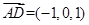 ,
,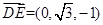 ,
, 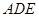 的法向量为
的法向量为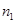
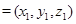 ,则
,则 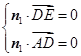
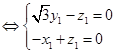 ,
,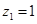 ,则
,则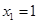 ,
,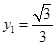 .所以
.所以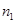
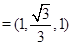 .
. 的法向量为
的法向量为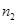
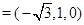 ,设平面
,设平面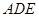 与平面
与平面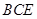 所成的锐二面角为
所成的锐二面角为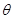 ,则
,则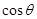
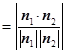
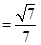 .
.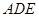 与平面
与平面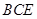 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为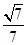 .
.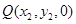 ,因为
,因为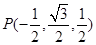 ,
,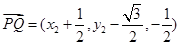 ,
,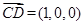 ,
,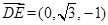 .
.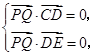 即
即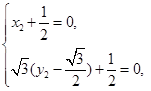
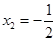 ,
,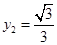 .
.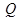 在三角形
在三角形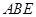 内的条件.
内的条件.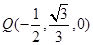 ,使
,使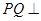 平面
平面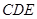 ,此时
,此时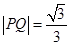 .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:高中数学 来源:不详 题型:解答题
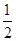 BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).
BC,∠ABC=60°,N是BC的中点,将梯形ABCD绕AB旋转90°,得到梯形ABC′D′(如图).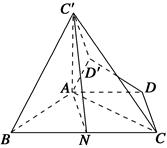
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
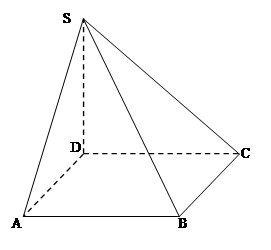
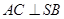 ;(2)求直线
;(2)求直线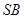 与平面
与平面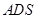 所成角的正弦值.
所成角的正弦值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
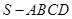 中,底面
中,底面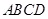 为平行四边形,侧面
为平行四边形,侧面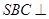 面
面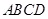 ,已知
,已知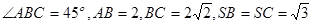
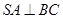 ;
;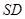 与面
与面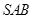 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
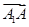 +
+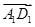 +
+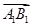 )2=3
)2=3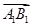 2;②
2;②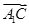 ·(
·(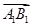 -
-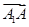 )=0;③向量
)=0;③向量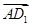 与向量
与向量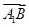 的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|
的夹角是60°;④正方体ABCD-A1B1C1D1的体积为|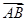 ·
·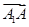 ·
·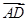 |.其中正确命题的序号是________.
|.其中正确命题的序号是________.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
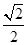 ,则下列结论中错误的是 ( ).
,则下列结论中错误的是 ( ).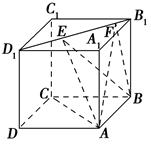
| A.AC⊥BE |
| B.EF∥平面ABCD |
| C.三棱锥A-BEF的体积为定值 |
| D.异面直线AE,BF所成的角为定值 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com