
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1)设椭圆![]() 的焦距为
的焦距为![]() ,可得出点
,可得出点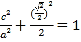 在椭圆
在椭圆![]() 上,将这个点的坐标代入椭圆
上,将这个点的坐标代入椭圆![]() 的方程可得出
的方程可得出![]() ,结合
,结合![]() 可求出
可求出![]() 的值,从而可得出椭圆
的值,从而可得出椭圆![]() 的标准方程;
的标准方程;
(2)分直线![]() 的斜率不存在与存在两种情况讨论,在
的斜率不存在与存在两种情况讨论,在![]() 轴时,可得出
轴时,可得出![]() ,从而求出
,从而求出![]() 的面积;在直线
的面积;在直线![]() 斜率存在时,设直线
斜率存在时,设直线![]() 的方程为
的方程为![]() ,设点
,设点![]() 、
、![]() ,将直线
,将直线![]() 的方程与椭圆方程联立,利用韦达定理结合
的方程与椭圆方程联立,利用韦达定理结合![]() ,得出
,得出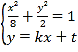 ,计算出
,计算出![]() 与
与![]() 的高,可得出
的高,可得出![]() 面积的表达式,然后可利用二次函数的基本性质求出
面积的表达式,然后可利用二次函数的基本性质求出![]() 面积的最大值.
面积的最大值.
(1)设椭圆![]() 的焦距为
的焦距为![]() ,由题知,点
,由题知,点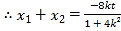 ,
,![]() ,
,
则有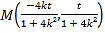 ,
,![]() ,又
,又![]() ,
,![]() ,
,![]() ,
,
因此,椭圆![]() 的标准方程为
的标准方程为![]() ;
;
(2)当![]() 轴时,
轴时,![]() 位于
位于![]() 轴上,且
轴上,且![]() ,
,
由![]() 可得
可得![]() ,此时
,此时![]() ;
;
当![]() 不垂直
不垂直![]() 轴时,设直线
轴时,设直线![]() 的方程为
的方程为![]() ,与椭圆交于
,与椭圆交于![]() ,
,![]() ,
,
由 ,得
,得![]() .
.
![]() ,
,![]() ,从而
,从而![]()
已知![]() ,可得
,可得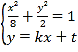 .
.
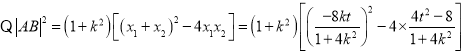
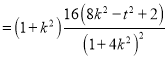 .
.
设![]() 到直线
到直线![]() 的距离为
的距离为![]() ,则
,则![]() ,
,
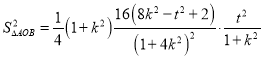 .
.
将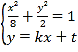 代入化简得
代入化简得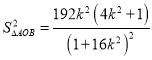 .
.
令![]() ,
,
则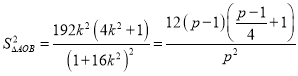
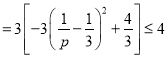 .
.
当且仅当![]() 时取等号,此时
时取等号,此时![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.
综上:![]() 的面积最大,最大值为
的面积最大,最大值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦点与双曲线
的焦点与双曲线![]() 的焦点重合,并且经过点
的焦点重合,并且经过点![]() .
.
(Ⅰ)求椭圆C的标准方程;
(II) 设椭圆C短轴的上顶点为P,直线![]() 不经过P点且与
不经过P点且与![]() 相交于
相交于![]() 、
、![]() 两点,若直线PA与直线PB的斜率的和为
两点,若直线PA与直线PB的斜率的和为![]() ,判断直线
,判断直线![]() 是否过定点,若是,求出这个定点,否则说明理由.
是否过定点,若是,求出这个定点,否则说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴,离心率为
轴,离心率为![]() ,短轴长为2.
,短轴长为2.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设![]() ,过椭圆
,过椭圆![]() 左焦点
左焦点![]() 的直线
的直线![]() 交
交![]() 于
于![]() ,
,![]() 两点,若对满足条件的任意直线
两点,若对满足条件的任意直线![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
,![]() 是两条不同的直线,
是两条不同的直线,![]() ,
,![]() ,
,![]() 是三个不同的平面,给出下列四个命题:
是三个不同的平面,给出下列四个命题:
①若![]() ,
,![]() ,则
,则![]()
②若![]() ,
,![]() ,
,![]() ,则
,则![]()
③若![]() ,
,![]() ,则
,则![]()
④若![]() ,
,![]() ,则
,则![]()
其中正确命题的序号是( )
A.①和②B.②和③C.③和④D.①和④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)阅读以下案例,利用此案例的想法化简![]() .
.
案例:考察恒等式![]() 左右两边
左右两边![]() 的系数.
的系数.
因为右边![]() ,
,
所以,右边![]() 的系数为
的系数为![]() ,
,
而左边![]() 的系数为
的系数为![]() ,
,
所以![]() =
=![]() .
.
(2)求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在
在![]() 处的切线的斜率为3,求实数
处的切线的斜率为3,求实数![]() 的值;
的值;
(2)若函数在区间![]() 上存在极小值,求实数
上存在极小值,求实数![]() 的取值范围;
的取值范围;
(3)如果![]() 的解集中只有一个整数,求实数
的解集中只有一个整数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】过去大多数人采用储蓄的方式将钱储蓄起来,以保证自己生活的稳定,考虑到通货膨胀的压力,如果我们把所有的钱都用来储蓄,这并不是一种很好的方式,随着金融业的发展,普通人能够使用的投资理财工具也多了起来,为了研究某种理财工具的使用情况,现对![]() 年龄段的人员进行了调查研究,将各年龄段人数分成
年龄段的人员进行了调查研究,将各年龄段人数分成![]() 组:
组:![]() ,并整理得到频率分布直方图:
,并整理得到频率分布直方图:
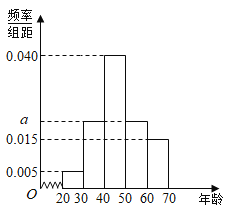
(1)求图中的![]() 值;
值;
(2)采用分层抽样的方法,从第二组、第三组、第四组中共抽取![]() 人,则三个组中各抽取多少人?
人,则三个组中各抽取多少人?
(3)在(2)中抽取的![]() 人中,随机抽取
人中,随机抽取![]() 人,则这
人,则这![]() 人都来自于第三组的概率是多少?
人都来自于第三组的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的长轴长是短轴长的2倍,且过点
的长轴长是短轴长的2倍,且过点![]() .
.
⑴求椭圆![]() 的方程;
的方程;
⑵若在椭圆上有相异的两点![]() (
(![]() 三点不共线),
三点不共线),![]() 为坐标原点,且直线
为坐标原点,且直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率满足
的斜率满足![]() .
.
(ⅰ)求证: ![]() 是定值;
是定值;
(ⅱ)设![]() 的面积为
的面积为![]() ,当
,当![]() 取得最大值时,求直线
取得最大值时,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com