
【题目】
A.(1,3)
B.(1, 4)
C.(2,3)
D.(2,4)
【答案】D
【解析】显然当直线f的斜率不存在时,必有两条直线满足题设.当直线l的斜率存在时,设斜率为k .设A(x1, y1), B(x2, y2), x1≠x2 , M(x0, y0), 则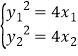 ,相减得(y1+y2)(y1-y2)=4(x1-x2), 由于x1≠x2 , 所以
,相减得(y1+y2)(y1-y2)=4(x1-x2), 由于x1≠x2 , 所以![]() , 即ky0=2, 圆心为C(5,0),由CM⊥AB,得k·
, 即ky0=2, 圆心为C(5,0),由CM⊥AB,得k·![]() =-1, ky0=5- x0. 所以2=5- x0 , x0=3, 即点M必在直线x=3上将x=3代入y2=4x得y2=12, ∴-2
=-1, ky0=5- x0. 所以2=5- x0 , x0=3, 即点M必在直线x=3上将x=3代入y2=4x得y2=12, ∴-2![]() <y0<2
<y0<2![]() . 因为点M在圆(x-5)2+y2=r2(r>0)上, 所以(x0-5)2+y02=r2 , r2=y02+4<12+4=16, 又y02+4>4(由于斜率不存在, 故y0≠0, 所以不取等号),所以4<y02+4<16, 所以2<r<4, 选D。
. 因为点M在圆(x-5)2+y2=r2(r>0)上, 所以(x0-5)2+y02=r2 , r2=y02+4<12+4=16, 又y02+4>4(由于斜率不存在, 故y0≠0, 所以不取等号),所以4<y02+4<16, 所以2<r<4, 选D。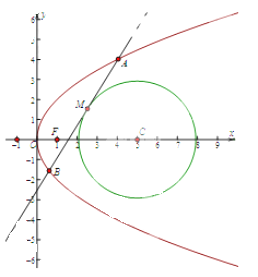


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,2ln2)
(a∈R)在x=2处的切线经过点(﹣4,2ln2)
(1)讨论函数f(x)的单调性
(2)若不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.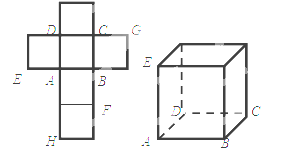
(1)请按字母F , G , H标记在正方体相应地顶点处(不需要说明理由)
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论.
(3)证明:直线DF⊥平面BEG
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·四川)一个正方体的平面展开图及该正方体的直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N.
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由)
(2)证明:直线MN∥平面BDH。
(3)求二面角A-EG-M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(2015·陕西)随机抽取一个年份,对西安市该年4月份的天气情况进行统计,结果如下:
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
天气 | 晴 | 雨 | 阴 | 阴 | 阴 | 雨 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 晴 |
日期 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
天气 | 晴 | 阴 | 雨 | 阴 | 阴 | 晴 | 阴 | 晴 | 晴 | 晴 | 阴 | 晴 | 晴 | 晴 | 雨 |
(1)在4月份任取一天,估计西安市在该天不下雨的概率;
(2)西安市某学校拟从4月份的一个晴天开始举行连续两天的运动会,估计运动会期间不下雨的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 已知函数
已知函数![]() .
.
(1)求函数![]() 的最小正周期;
的最小正周期;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移a(a>0)个单位长度后得到函数
个单位长度,再向下平移a(a>0)个单位长度后得到函数![]() 的图象,且函数
的图象,且函数![]() 的最大值为2.
的最大值为2.
(ⅰ)求函数![]() 的解析式;
的解析式;
(ⅱ)证明:存在无穷多个互不相同的正整数![]() ,使得
,使得![]() >0.
>0.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com