
【题目】某个命题与自然数n有关,如果当![]() (
(![]() )时该命题成立,则可得
)时该命题成立,则可得![]() 时该命题也成立,若已知
时该命题也成立,若已知![]() 时命题不成立,则下列说法正确的是______(填序号)
时命题不成立,则下列说法正确的是______(填序号)
(1)![]() 时,该命题不成立;
时,该命题不成立;
(2)![]() 时,该命题不成立;
时,该命题不成立;
(3)![]() 时,该命题可能成立;
时,该命题可能成立;
(4)![]() 时,该命题可能成立也可能不成立,但若
时,该命题可能成立也可能不成立,但若![]() 时命题成立,则对任意
时命题成立,则对任意![]() ,该命题都成立.
,该命题都成立.
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以直角坐标系的原点
为参数),以直角坐标系的原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系.
轴正半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)设曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,求三条曲线
,求三条曲线![]() ,
,![]() ,
,![]() 所围成图形的面积.
所围成图形的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】折纸与数学有着千丝万缕的联系,吸引了人们的广泛兴趣.因![]() 纸的长宽比
纸的长宽比![]() 称为白银分割比例,故
称为白银分割比例,故![]() 纸有一个白银矩形的美称.现有一张如图1所示的
纸有一个白银矩形的美称.现有一张如图1所示的![]() 纸
纸![]() ,
,![]() .
.
![]() 分别为
分别为![]() 的中点,将其按折痕
的中点,将其按折痕![]() 折起(如图2),使得
折起(如图2),使得![]() 四点重合,重合后的点记为
四点重合,重合后的点记为![]() ,折得到一个如图3所示的三棱锥
,折得到一个如图3所示的三棱锥![]() .记
.记![]() 为
为![]() 的中点,在
的中点,在![]() 中,
中,![]() 为
为![]() 边上的高.
边上的高.
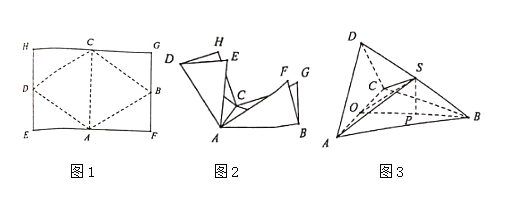
(1)求证:![]() 平面
平面![]() ;
;
(2)若![]() 分别是棱
分别是棱![]() 上的动点,且
上的动点,且![]() .当三棱锥
.当三棱锥![]() 的体积最大时,求平面
的体积最大时,求平面![]() 与平面
与平面![]() 所成锐二面角的余弦值.
所成锐二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),以坐标原点
),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程是
的极坐标方程是![]() .
.
(1)求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知矩形![]() 所在平面与半圆弧
所在平面与半圆弧![]() 所在平面垂直,
所在平面垂直,![]() 是半圆弧
是半圆弧![]() 上异于
上异于![]() ,
,![]() 的点.
的点.
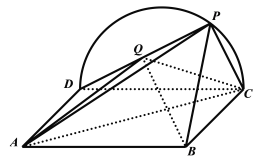
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,当三棱锥
,当三棱锥![]() 的体积最大且二面角
的体积最大且二面角![]() 的平面角的大小为
的平面角的大小为![]() 时,试确定
时,试确定![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a,b,c分别为△ABC三个内角A,B,C的对边,且acos C+![]() asin C-b-c=0.
asin C-b-c=0.

(1)求A;
(2)若AD为BC边上的中线,cos B=![]() ,AD=
,AD=![]() ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com