
【题目】设整数![]() 满足
满足![]() .记
.记![]() .求f的最小值f0.并确定使f=f0成立的数组
.求f的最小值f0.并确定使f=f0成立的数组![]() 的个数.
的个数.
【答案】![]() ;
;![]() 个.
个.
【解析】
根据题设条件,化简得到![]() ,在结合二次函数的性质,即可求得
,在结合二次函数的性质,即可求得![]() 最小值,再由对每个k(1≤k≤49),设
最小值,再由对每个k(1≤k≤49),设![]() 等于k的项数为
等于k的项数为![]() ,结合方程的正整数解
,结合方程的正整数解![]() 的组数,即可求解.
的组数,即可求解.
由题意,![]() ,
,
可得![]() ,
,![]() ①
①
由于![]() 及
及![]() 均为非负整数,故有
均为非负整数,故有![]() ,
,
且![]() ,
,
于是![]()
![]() ,
,![]() ②
②
由①,②得![]() ,
,
结合![]() 及
及![]() ,
,
可知![]()
![]() ,
,![]() ③
③
另一方面,令![]() ,
,![]() ,
,![]() ,
,
此时验证,知上述所有不等式均取到等号,从而f的最小值![]() .
.
以下考虑③的取等条件.此时![]() ,且②中的不等式均取等,
,且②中的不等式均取等,
即![]() .
.
因此![]() ,且对每个k(1≤k≤49),
,且对每个k(1≤k≤49),![]() 中至少有两项等于k.易验证,知这也是③取等的充分条件.
中至少有两项等于k.易验证,知这也是③取等的充分条件.
对每个k(1≤k≤49),设![]() 等于k的项数为
等于k的项数为![]() ,
,
则nk为正整数,且![]() ,
,
即![]() ,
,
该方程的正整数解![]() 的组数为
的组数为![]() ,
,
且每组解唯一对应一个使④取等的数组![]() ,
,
故使![]() 成立的数组
成立的数组![]() 有
有![]() 个.
个.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)=ex﹣ax2﹣ax,h(x)=ex﹣2x﹣lnx.其中e为自然对数的底数.
(1)若f(x)=h(x)﹣g(x).
①讨论f(x)的单调性;
②若函数f(x)有两个不同的零点,求实数a的取值范围.
(2)已知a>0,函数g(x)恰有两个不同的极值点x1,x2,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
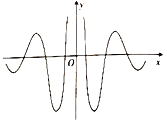
【题目】著名数学家华罗庚先生曾说过:“数缺形时少直观,形缺数时难入微数形结合百般好,隔裂分家万事休.”在数学的学习和研究中,我们经常用函数的图象来研究函数的性质,也经常用函数的解析式来琢磨函数的图象的特征,如某体育品牌的LOGO为![]() ,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
,可抽象为如图所示的轴对称的优美曲线,下列函数中,其图象大致可“完美”局部表达这条曲线的函数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为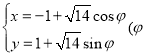 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .曲线
.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 与曲线
与曲线![]() 的交线为直线
的交线为直线![]() .
.
(1)求直线![]() 和曲线
和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与曲线
,与曲线![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求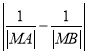 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 的图象的一条对称轴为
的图象的一条对称轴为![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A.![]() 是最小正周期为
是最小正周期为![]() 的奇函数
的奇函数
B.![]() 是
是![]() 图像的一个对称中心
图像的一个对称中心
C.![]() 在
在![]() 上单调递增
上单调递增
D.先将函数![]() 图象上各点的纵坐标缩短为原来的
图象上各点的纵坐标缩短为原来的![]() ,然后把所得函数图象再向左平移
,然后把所得函数图象再向左平移![]() 个单位长度,即可得到函数
个单位长度,即可得到函数![]() 的图象.
的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]()
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,证明曲线
时,证明曲线![]() 分别在点
分别在点![]() 和点
和点![]() 处的切线为不同的直线;
处的切线为不同的直线;
(3)已知过点![]() 能作曲线
能作曲线![]() 的三条切线,求
的三条切线,求![]() ,
,![]() 所满足的条件.
所满足的条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有9位身高各异的同学拍照留念,分成前后两排,前排4人,后排5人,要求每排同学的身高从中间到两边依次递减,则不同的排队方式有________种.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com