
【题目】已知函数![]() .
.
(1)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的最小值;
的最小值;
(2)若存在![]() ,
,![]() ,使
,使![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:
【题目】已知定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,且
,且![]() ,则下列说法正确的有( )
,则下列说法正确的有( )
(1)若函数![]() ,则函数
,则函数![]() 是奇函数;
是奇函数;
(2)![]() ;
;
(3)设函数![]() ,则函数
,则函数![]() 的图象经过点
的图象经过点![]() ;
;
(4)设![]() ,若数列
,若数列![]() 是等比数列,则
是等比数列,则![]() .
.
A.(2)(3)(4)B.(1)(3)(4)C.(1)(3)D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中数学 来源: 题型:
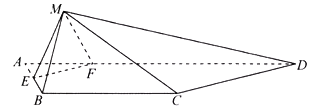
【题目】如图,在等腰梯形ABCD中,AD∥BC,AB=BC=CD=1,AD=2,点E、F分别在线段AB、AD上,且EF∥CD,将△AEF沿EF折起到△MEF的位置,并使平面MEF⊥平面BCDFE,得到几何体M﹣BCDEF,则折叠后的几何体的体积的最大值为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学棋艺协会定期举办“以棋会友”的竞赛活动,分别包括“中国象棋”、“围棋”、“五子棋”、“国际象棋”四种比赛,每位协会会员必须参加其中的两种棋类比赛,且各队员之间参加比赛相互独立;已知甲同学必选“中国象棋”,不选“国际象棋”,乙同学从四种比赛中任选两种参与.
(1)求甲参加围棋比赛的概率;
(2)求甲、乙两人参与的两种比赛都不同的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是抛物线
是抛物线![]() 的焦点,恰好又是双曲线
的焦点,恰好又是双曲线![]() 的右焦点,双曲线
的右焦点,双曲线![]() 过点
过点![]() ,且其离心率为
,且其离心率为![]() .
.
(1)求抛物线![]() 和双曲线
和双曲线![]() 的标准方程;
的标准方程;
(2)已知直线![]() 过点
过点![]() ,且与抛物线
,且与抛物线![]() 交于
交于![]() ,
,![]() 两点,以
两点,以![]() 为直径作圆
为直径作圆![]() ,设圆
,设圆![]() 与
与![]() 轴交于点
轴交于点![]() ,
,![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面直角坐标系中,直线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数).以原点为极点,
为参数).以原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出直线![]() 的极坐标方程与曲线
的极坐标方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知与直线![]() 平行的直线
平行的直线![]() 过点
过点![]() ,且与曲线
,且与曲线![]() 交于
交于![]() 两点,试求
两点,试求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com