
分析 (Ⅰ)推导出a3=|a2|-a0=|a2|,a4=|a3|-a2=|a2|-a2,由此能求出a3,a5的值.
(Ⅱ)假设P数列{an}的项都是正数,则an+2=an+1-an,an+3=an+2-an+1=-an<0,与假设矛盾;假设P数列{an}的项都是负数,则an+2=|an+1|-an>0,与假设矛盾,由此能证明{an}的项不可能全是正数,也不可能全是负数.
(Ⅲ)存在最小的正整数k满足ak<0,ak+1>0(k≤5),数列{an}是周期为9的数列,由此能求出结果.
解答 解:(Ⅰ)因为{an}是P数列,且a1=0,
所以a3=|a2|-a0=|a2|,
所以a4=|a3|-a2=|a2|-a2,
所以|a2|-a2=1,解得${a_2}=-\frac{1}{2}$….(1分)
所以${a_3}=\frac{1}{2},{a_5}=|{a_4}|-{a_3}=\frac{1}{2}$.….(3分)
证明:(Ⅱ)假设P数列{an}的项都是正数,即an>0,an+1>0,an+2>0,
所以an+2=an+1-an,an+3=an+2-an+1=-an<0,与假设矛盾.
故P数列{an}的项不可能全是正数,….(5分)
假设P数列{an}的项都是负数,
则an<0,而an+2=|an+1|-an>0,与假设矛盾,….7分
故P数列{an}的项不可能全是负数.
解:(Ⅲ)由(Ⅱ)可知P数列{an}中项既有负数也有正数,
且最多连续两项都是负数,最多连续三项都是正数.
因此存在最小的正整数k满足ak<0,ak+1>0(k≤5).
设ak=-a,ak+1=b(a,b>0),
则ak+2=b+a,ak+3=a,ak+4=-b,ak+5=b-a.ak+6=|b-a|+b,ak+7=|b-a|+a,ak+8=a-b,ak+9=-a,ak+10=b,
故有ak=ak+9,即数列{an}是周期为9的数列….(9分)
由上可知ak,ak+1,…,ak+8这9项中,
ak,ak+4为负数,ak+5,ak+8这两项中一个为正数,另一个为负数,其余项都是正数.
因为2016=9×224,
所以当k=1时,m=224×3=672;
当2≤k≤5时,a1,a2,…,ak-1这k-1项中至多有一项为负数,而且负数项只能是ak-1,
记ak,ak+1,…,a2016这2007-k项中负数项的个数为t,
当k=2,3,4时,若ak-1<0,则b=ak+1=|ak|-ak-1>|ak|=a,故ak+8为负数,
此时t=671,m=671+1=672;
若ak-1>0,则b=ak+1=|ak|-ak-1<|ak|=a,故ak+5为负数.
此时t=672,m=672,
当k=5时,ak-1必须为负数,t=671,m=672,….(12分)
综上可知m的取值集合为{672}.….(13分)
点评 本题考查数列中第3项和第5项的求法,考查数列中的项不可能全是正数,也不可能全是负数的证明,考查实数的集合的求法,是中档题,解题时要认真审题,注意数列性质的合理运用.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
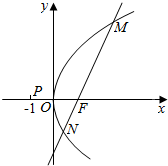 已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.
已知点F为抛物线C:y2=2px(p>0)的焦点,过点F的动直线l与抛物线C交于M,N两点,如图.当直线l与x轴垂直时,|MN|=4.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a>b,则ac2>bc2 | |
| B. | 若x≠0,则x+$\frac{4}{x}$的最小值为4 | |
| C. | “φ=$\frac{π}{2}$”是函数y=sin(x+φ)为偶函数“的充要条件 | |
| D. | 命题“?x>0,x-lnx>0”的否定是“?x0>0,x0-lnx0≤0” |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com