
【题目】网购已经成为一种时尚,商家为了鼓励消费,购买时在店铺领取优惠券,买后给予好评返还现金等促销手段.经统计,近五年某店铺用于促销的费用![]() (万元)与当年度该店铺的销售收人
(万元)与当年度该店铺的销售收人![]() (万元)的数据如下表:
(万元)的数据如下表:
年份 | 2013年 | 2014年 | 2015年 | 2016年 | 2017年 |
促销费用 |
|
|
|
|
|
销售收入 |
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出/span>![]() 关于
关于![]() 的线性回归方
的线性回归方![]() ;
;
(2)2018年度该店铺预测销售收人至少达到![]() 万元,则该店铺至少准备投入多少万元的促销费?
万元,则该店铺至少准备投入多少万元的促销费?
参考公式: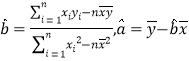
参考数据: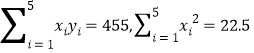
科目:高中数学 来源: 题型:
【题目】若定义在![]() 上的函数
上的函数![]() ,其图象是连续不断的,且存在常数
,其图象是连续不断的,且存在常数![]() 使得
使得![]() 对任意的实数
对任意的实数![]() 都成立,则称
都成立,则称![]() 是一个“
是一个“![]() 特征函数”则下列结论中正确的个数为( ).
特征函数”则下列结论中正确的个数为( ).
①![]() 是常数函数中唯一的“
是常数函数中唯一的“![]() 特征函数”;
特征函数”;
②![]() 不是“
不是“![]() 特征函数”;
特征函数”;
③“![]() 特征函数”至少有一个零点;
特征函数”至少有一个零点;
④![]() 是一个“
是一个“![]() 特征函数”;.
特征函数”;.
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】桑基鱼塘是某地一种独具地方特色的农业生产形式,某研究单位打算开发一个桑基鱼塘项目,该项目准备购置一块![]() 平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为
平方米的矩形地块,中间挖成三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,池塘周围的基围宽均为![]() 米,如图,设池塘所占总面积为
米,如图,设池塘所占总面积为![]() 平方米.
平方米.
(Ⅰ)试用![]() 表示
表示![]() .
.
(Ⅱ)当![]() 取何值时,才能使得
取何值时,才能使得![]() 最大?并求出
最大?并求出![]() 的最大值.
的最大值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,且过点
,且过点![]() .
.
(![]() )求椭圆
)求椭圆![]() 的标准方程.
的标准方程.
(![]() )
)![]() 、
、![]() 、
、![]() 、
、![]() 是椭圆
是椭圆![]() 上的四个不同的点,两条都不和
上的四个不同的点,两条都不和![]() 轴垂直的直线
轴垂直的直线![]() 和
和![]() 分别过点
分别过点![]() ,
, ![]() ,且这条直线互相垂直,求证:
,且这条直线互相垂直,求证: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】树立和践行“绿水青山就是金山银山,坚持人与自然和谐共生”的理念越来越深入人心,已形成了全民自觉参与,造福百姓的良性循环.据此,某网站推出了关于生态文明建设进展情况的调查,调查数据表明,环境治理和保护问题仍是百姓最为关心的热点,参与调查者中关注此问题的约占![]() .现从参与关注生态文明建设的人群中随机选出
.现从参与关注生态文明建设的人群中随机选出![]() 人,并将这
人,并将这![]() 人按年龄分组:第
人按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)求出![]() 的值;
的值;
(Ⅱ)求出这![]() 人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
人年龄的样本平均数(同一组数据用该区间的中点值作代表)和中位数(精确到小数点后一位);
(Ⅲ)现在要从年龄较小的第![]() 、
、![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,则第
人,则第![]() 、
、![]() 组分别抽取多少人?
组分别抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设双曲线C的焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,其一个顶点的坐标是(0,1).
,其一个顶点的坐标是(0,1).
(Ⅰ)求双曲线C的标准方程;
(Ⅱ)若直线![]() 与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线
与该双曲线交于A、B两点,且A、B的中点为(2,3),求直线![]() 的方程
的方程
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com