
【题目】某市一高中经过层层上报,被国家教育部认定为2015年全国青少年足球特色学校.该校成立了特色足球队,队员来自高中三个年级,人数为50人.视力对踢足球有一定的影响,因而对这50人的视力作一调查.测量这50人的视力(非矫正视力)后发现他们的视力全部介于4.75和5.35之间,将测量结果按如下方式分成6组:第一组[4.75,4.85),第二组[4.85,4.95),…,第6组[5.25,5.35],如图是按上述分组方法得到的频率分布直方图.又知:该校所在的省中,全省喜爱足球的高中生视力统计调查数据显示:全省100000名喜爱足球的高中生的视力服从正态分布N(5.01,0.0064). 参考数据:若ξ~N(μ,σ2),则P(μ﹣σ<ξ≤μ+σ)=0.6826,
P(μ﹣2σ<ξ≤μ+2σ)=0.9544,P(μ﹣3σ<ξ≤μ+3σ)=0.9974.
(1)试评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况; 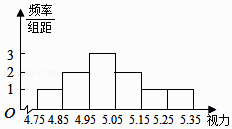
(2)求这50名队员视力在5.15以上(含5.15)的人数;
(3)在这50名队员视力在5.15以上(含5.15)的人中任意抽取2人,该2人中视力排名(从高到低)在全省喜爱足球的高中生中前130名的人数记为ξ,求ξ的数学期望.
【答案】
(1)解:由频率分布直方图知,
该校特色足球队人员平均视力为4.8 0.1+4.9 0.2+5.0 0.3+5.1 0.2+5.2 0.1+5.3 0.1=5.03
高于全省喜爱足球的高中生的平均值5.01
(2)解:由频率分布直方图知,后两组队员的视力在5.15以上(含5.15),其频率为0.2,人数为0.2 50=10,
即这50名队员视力在5.15以上(含5.15)的人数为10人
(3)解:∵P(5.01﹣3×0.08<ξ≤5.01﹣3×0.08,即P(4.77<ξ≤5.25)=0.9974,
∴P(ξ≥5.25)= ![]() =0.013,0.0013×100000=130,
=0.013,0.0013×100000=130,
∴全省喜爱足球的高中生中前130名的视力在5.25以上.这50人中视力在5.25以上的有0.1 50=5人,
这50名队员视力在5.15以上(含5.15)的人分为两部分:5人在5.25以上,5人在5.15∽5.25
随机变量ξ可取0,1,2,
P(ξ=0)= ![]() =
= ![]() =
= ![]() ,
,
P(ξ=1)= ![]() =
= ![]() =
= ![]() ,
,
P(ξ=2)= ![]() =
= ![]() =
= ![]() .
.
∴Eξ=0× ![]() +1×
+1× ![]() +2×
+2× ![]() =1
=1
【解析】(1)由频率分布直方图求出该校特色足球队人员平均视力,由此能评估该校特色足球队人员在全省喜爱足球的高中生中的平均视力状况.(2)由频率分布直方图求出后两组队员的视力在5.15以上(含5.15),其频率为及人数.(3)由题意随机变量ξ可取0,1,2,分别求出相应的概率,由此能求出ξ的数学期望.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某中学食堂定期从粮店以每吨1500元的价格购买大米,每次购进大米需支付运输费 100元.食堂每天需用大米l吨,贮存大米的费用为每吨每天2元(不满一天按一天计),假 定食堂每次均在用完大米的当天购买.
(1)该食堂隔多少天购买一次大米,可使每天支付的总费用最少?
(2)粮店提出价格优惠条件:一次购买量不少于20吨时,大米价格可享受九五折(即原价的95%),问食堂可否接受此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有一块半径为 ![]() (
( ![]() 是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
是正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 ![]() 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰 ![]() ,其中
,其中 ![]() 为圆心,
为圆心, ![]() ,
, ![]() 在圆的直径上,
在圆的直径上, ![]() ,
, ![]() ,
, ![]() 在半圆周上,如图.设
在半圆周上,如图.设 ![]() ,征地面积为
,征地面积为 ![]() ,当
,当 ![]() 满足
满足 ![]() 取得最大值时,开发效果最佳,开发效果最佳的角
取得最大值时,开发效果最佳,开发效果最佳的角 ![]() 和
和 ![]() 的最大值分别为( )
的最大值分别为( )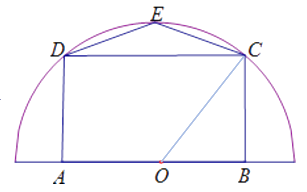
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设甲、乙两人每次射击命中目标的概率分别为 ![]() ,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
,且各次射击相互独立,若按甲、乙、甲、乙…的次序轮流射击,直到有一人击中目标就停止射击,则停止射击时,甲射击了两次的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设 ![]() ,
, ![]() 是平面
是平面 ![]() 的一组基底,则能作为平面
的一组基底,则能作为平面 ![]() 的一组基底的是( )
的一组基底的是( )
A.![]() ﹣
﹣ ![]() ,
, ![]() ﹣
﹣ ![]()
B.![]() +2
+2 ![]() ,
, ![]() +
+ ![]()
C.2 ![]() ﹣3
﹣3 ![]() ,6
,6 ![]() ﹣4
﹣4 ![]()
D.![]() +
+ ![]() ,
, ![]() ﹣
﹣ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)=Asin(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( ) 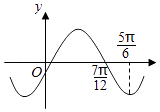
A.向左平移 ![]() 个单位长度
个单位长度
B.向左平移 ![]() 个单位长度
个单位长度
C.向右平移 ![]() 个单位长度
个单位长度
D.向右平移 ![]() 个单位长度
个单位长度
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设M=10a2+81a+207,P=a+2,Q=26﹣2a,若将lgM,lgQ,lgP适当排序后可构成公差为1的等差数列{an}的前三项. (Ⅰ)求a的值及{an}的通项公式;
(Ⅱ)记函数 ![]() 的图像在x轴上截得的线段长为bn , 设
的图像在x轴上截得的线段长为bn , 设 ![]() ,求Tn .
,求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项为1,前n项和Sn与an之间满足an= ![]() (n≥2,n∈N*)
(n≥2,n∈N*)
(1)求证:数列{ ![]() }是等差数列;
}是等差数列;
(2)求数列{an}的通项公式;
(3)设存在正整数k,使(1+S1)(1+S1)…(1+Sn)≥k ![]() 对于一切n∈N*都成立,求k的最大值.
对于一切n∈N*都成立,求k的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等比数列{an}满足an>0,n=1,2,…,且a5a2n﹣5=22n(n≥3),则当n≥1时,log2a1+log2a3+…+log2a2n﹣1=( )
A.n(2n﹣1)
B.(n+1)2
C.n2
D.(n﹣1)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com