
【题目】已知函数![]() ,若存在
,若存在![]() ,使得关于
,使得关于![]() 的方程
的方程![]() 有三个不等实根,则实数
有三个不等实根,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知四面体有五条棱长为3,且外接球半径为2.动点P在四面体的内部或表面,P到四个面的距离之和记为s.已知动点P在![]() ,
,![]() 两处时,s分别取得最小值和最大值,则线段
两处时,s分别取得最小值和最大值,则线段![]() 长度的最小值为______.
长度的最小值为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国历法中将一年分为春、夏、秋、冬四个季节,每个季节有六个节气,如夏季包含立夏、小满、芒种、夏至、小暑以及大暑.某美术学院甲、乙、丙、丁四位同学接到绘制二十四节气的彩绘任务,现四位同学抽签确定各自完成哪个季节中的六幅彩绘,在制签及抽签公平的前提下,甲没有抽到绘制春季六幅彩绘任务且乙没有抽到绘制夏季六幅彩绘任务的概率为_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】向量集合![]() ,对于任意
,对于任意![]() ,以及任意
,以及任意![]() ,都有
,都有![]() ,则称
,则称![]() 为“
为“![]() 类集”,现有四个命题:
类集”,现有四个命题:
①若![]() 为“
为“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
②若![]() ,
,![]() 都是“
都是“![]() 类集”,则集合
类集”,则集合![]() 也是“
也是“![]() 类集”;
类集”;
③若![]() 都是“
都是“![]() 类集”,则
类集”,则![]() 也是“
也是“![]() 类集”;
类集”;
④若![]() 都是“
都是“![]() 类集”,且交集非空,则
类集”,且交集非空,则![]() 也是“
也是“![]() 类集”.
类集”.
其中正确的命题有________(填所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】人耳的听力情况可以用电子测听器检测,正常人听力的等级为![]() (分贝),并规定测试值在区间
(分贝),并规定测试值在区间![]() 为非常优秀,测试值在区间
为非常优秀,测试值在区间![]() 为优秀,某班
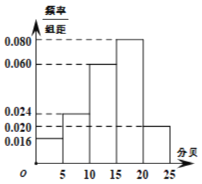
为优秀,某班![]() 名同学都进行了听力测试,所得测试值制成频率分布直方图:
名同学都进行了听力测试,所得测试值制成频率分布直方图:
(Ⅰ)现从听力等级为![]() 的同学中任意抽取出4人,记听力非常优秀的同学人数为
的同学中任意抽取出4人,记听力非常优秀的同学人数为![]() ,求
,求![]() 的分布列与数学期望:
的分布列与数学期望:
(Ⅱ)现选出一名同学参加另一项测试,测试规则如下:四个音叉的发生情况不同,由强到弱的次序分别为1,2,3,4.测试前将音叉随机排列,被测试的同学依次听完后给四个音叉按发音的强弱标出一组序号![]() (其中
(其中![]() 为1,2,3,4的一个排列),记
为1,2,3,4的一个排列),记![]() ,可用
,可用![]() 描述两次排序的偏离程度,求
描述两次排序的偏离程度,求![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,![]() 底面ABC,
底面ABC,![]() ,H为PC的中点,M为AH的中点
,H为PC的中点,M为AH的中点![]() ,
,![]() .
.
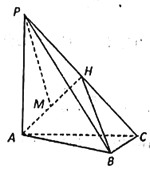
(1)求PM与平面AHB成角的正弦值;
(2)在线段PB上是否存在点N,使得![]() 平面ABC.若存在,请说明点N的位置,若不存在,请说明理由.
平面ABC.若存在,请说明点N的位置,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com