练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知圆.

    （1）若圆的切线在轴、轴上的截距相等，求切线的方程；

    （2）若点是圆C上的动点，求的取值范围.

    【答案】（1）或或；（2）

    【解析】

    （1）求出圆心和半径.当切线过原点时，设切线方程为，利用圆心到直线的距离等于半径，求得的值.当切线不过原点时，切线方程为，利用圆心到直线的距离等于半径，求得的值.

    （2）将问题转化为直线与圆有公共点，由圆心到直线的距离不大于半径列不等式，解不等式求得的取值范围.

    （1）由方程知圆心为，半径为，

    当切线过原点时，设切线方程为，则，

    ∴，即切线方程为.

    当切线不过原点时，设切线方程为，

    则，∴或，

    即切线方程为或.

    ∴切线方程为或或.

    （2）由题意可知，直线与圆有公共点，

    所以圆心到直线的距离.

    即，即的取值范围是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知向量，记．

    （1）若，求的值；

    （2）在锐角中，角的对边分别是，且满足，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】十九大提出，坚决打赢脱贫攻坚战，某帮扶单位为帮助定点扶贫村真脱贫，坚持扶贫同扶智相结合，帮助贫困村种植蜜柚，并利用电商进行销售，为了更好地销售，现从该村的蜜柚树上随机摘下了100个蜜柚进行测重，其质量分别在， ， ， ， ， （单位：克）中，其频率分布直方图如图所示.

    （1）按分层抽样的方法从质量落在， 的蜜柚中抽取5个，再从这5个蜜柚中随机抽取2个，求这2个蜜柚质量均小于2000克的概率；

    （2）以各组数据的中间数代表这组数据的平均水平，以频率代表概率，已知该贫困村的蜜柚树上大约还有5000个蜜柚等待出售，某电商提出两种收购方案：

    A.所有蜜柚均以40元/千克收购；

    B．低于2250克的蜜柚以60元/个收购，高于或等于2250克的以80元/个收购.

    请你通过计算为该村选择收益最好的方案.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】连结圆周上九个不同点的36条弦要么染成红色，要么染成蓝色，我们称它们为“红边”或“蓝边”.假定由这九个点中每三个点为顶点的三角形中都含有“红边”.证明：这九个点中存在四个点，两两连结的六条边都是红边.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知f（x）是定义在R上的偶函数，且在区间（﹣∞，0]上单调递增，若实数a满足f（log2|a﹣1|）＞f（﹣2），则a的取值范围是_____

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为自然底数），且.

    (1)当时，对任意的，都有不等式，求实数的取值范围；

    (2)若函数是上的减函数，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知数列和满足：,其中为实数，为正整数．

    （1）对任意实数，证明数列不是等比数列；

    （2）对于给定的实数，试求数列的前项和；

    （3）设，是否存在实数，使得对任意正整数，都有成立？若存在，求的取值范围；若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱锥V-ABC中，平面VAB⊥平面ABC，△VAB为等边三角形，AC⊥BC且AC=BC=，O，M分别为AB，VA的中点．

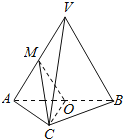
    （1）求证：VB∥平面MOC；

    （2）求证：平面MOC⊥平面VAB

    （3）求三棱锥V-ABC的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本题满分12分） 如图，的外接圆的半径为，所在的平面，，，，且，．

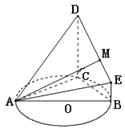
    （1）求证：平面ADC平面BCDE．

    （2）试问线段DE上是否存在点M，使得直线AM与平面ACD所成角的正弦值为？若存在，

    确定点M的位置，若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案