
【题目】已知函数f(x)=ax3+bx2的图象经过点M(1,4),曲线在点M处的切线恰好与直线x+9y=0垂直.
(1)求实数a,b的值;
(2)若函数f(x)在区间[m,m+1]上单调递增,求m的取值范围.
【答案】
(1)解:∵f(x)=ax3+bx2的图象经过点M(1,4),∴a+b=4①式 …(1分)
f'(x)=3ax2+2bx,则f'(1)=3a+2b
由条件 ![]() ②式
②式
由①②式解得a=1,b=3
(2)解:f(x)=x3+3x2,f'(x)=3x2+6x,
令f'(x)=3x2+6x≥0得x≥0或x≤﹣2,
∵函数f(x)在区间[m,m+1]上单调递增
∴[m,m+1](﹣∝,﹣2]∪[0,+∝)
∴m≥0或m+1≤﹣2
∴m≥0或m≤﹣3
【解析】(1)将M的坐标代入f(x)的解析式,得到关于a,b的一个等式;求出导函数,求出f′(1)即切线的斜率,利用垂直的两直线的斜率之积为﹣1,列出关于a,b的另一个等式,解方程组,求出a,b的值.(2)求出 f′(x),令f′(x)>0,求出函数的单调递增区间,据题意知[m,m+1](﹣∝,﹣2]∪[0,+∝),列出端点的大小,求出m的范围.
【考点精析】通过灵活运用导数的几何意义,掌握通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() 即可以解答此题.
即可以解答此题.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】每年的三月十二日,是中国的植树节,林管部门在植树前,为保证树苗的质量,都会在植树前对树苗进行检测.现从甲、乙两批树苗中各抽测了10株树苗的高度,规定高于128厘米的为“良种树苗”,测得高度如下(单位:厘米)
甲:137,121,131,120,129,119,132,123,125,133
乙:110,130,147,127,146,114,126,110,144,146
(1)根据抽测结果,完成答题卷中的茎叶图,并根据你填写的茎叶图,对甲、乙两批树苗的高度作比较,写出对两种树苗高度的统计结论;
(2)设抽测的10株甲种树苗高度平均值为 ![]() ,将这10株树苗的高度依次输入按程序框图进行运算,
,将这10株树苗的高度依次输入按程序框图进行运算,
(如图)问输出的S大小为多少?并说明S的统计学意义.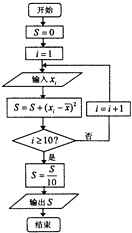
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥S﹣ABC中,∠ABC=90°,SA⊥平面ABC,点A在SB和SC上的射影分别为E、D. 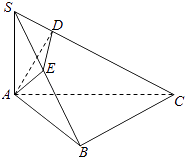
(1)求证:DE⊥SC;
(2)若SA=AB=BC=1,求直线AD与平面ABC所成角的余弦值. 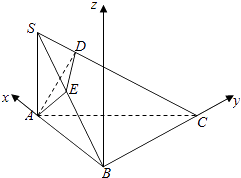
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C过点A(6,4),B(1,﹣1),且圆心在直线l:x﹣5y+7=0上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明1+2+3+…+n2= ![]() ,则当n=k+1时左端应在n=k的基础上加上( )
,则当n=k+1时左端应在n=k的基础上加上( )
A.k2+1
B.(k+1)2
C.![]()
D.(k2+1)+(k2+2)+(k2+3)+…+(k+1)2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() 的右焦点为
的右焦点为![]() ,右顶点为
,右顶点为![]() .已知
.已知![]() ,其中
,其中![]() 为原点,
为原点, ![]() 为椭圆的离心率.
为椭圆的离心率.
(1)求椭圆的方程及离心率![]() 的值;
的值;
(2)设过点![]() 的直线
的直线![]() 与椭圆交于点
与椭圆交于点![]() (
(![]() 不在
不在![]() 轴上),垂直于
轴上),垂直于![]() 的直线与
的直线与![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .若
.若![]() ,且
,且![]() ,求直线
,求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com