
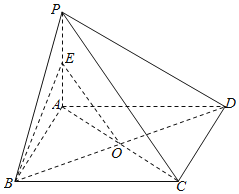
【题目】如图,在直角梯形![]() 中,
中,![]() ,点A是PB的中点,现沿AD将平面PAD折起,设
,点A是PB的中点,现沿AD将平面PAD折起,设![]() .
.

(1)当![]() 为直角时,求异面直线PC与BD所成角的大小;
为直角时,求异面直线PC与BD所成角的大小;
(2)当![]() 为多少时,三棱锥
为多少时,三棱锥![]() 的体积为
的体积为![]() ?
?
(3)剪去梯形中的![]() ,留下长方形纸片
,留下长方形纸片![]() ,在BC边上任取一点E,把纸片沿AE折成直二面角,问E点取何处时,使折起后两个端点
,在BC边上任取一点E,把纸片沿AE折成直二面角,问E点取何处时,使折起后两个端点![]() 间的距离最短.
间的距离最短.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)当
;(3)当![]() 时,沿AE折起后
时,沿AE折起后![]() 间距离最短
间距离最短
【解析】
(1)取PA的中点E,连结OE,BE,则∠BOP为PC,BD所成的角,先证 PA⊥平面ABCD,利用勾股定理求出![]() 的三边长,使用余弦定理求出
的三边长,使用余弦定理求出![]() ,进而可得角;(2)P到平面ABCD的距离为
,进而可得角;(2)P到平面ABCD的距离为![]() ,代入棱锥
,代入棱锥![]() 的体积公式求出
的体积公式求出![]() 得出θ的值;(3)设
得出θ的值;(3)设![]() ,则
,则![]() ,根据定理可得化简
,根据定理可得化简![]() ,故而当
,故而当![]() 时,
时,![]() 间的距离最短,故而可得结论.
间的距离最短,故而可得结论.
(1)∵AB∥CD,![]() ,
,![]() ,∴四边形ABCD是矩形,
,∴四边形ABCD是矩形,
连结AC交BD与O,则O是AC,BD的中点,
取PA的中点E,连结OE,BE,
则OE是![]() 的中位线,∴
的中位线,∴![]() ,
,![]() ,
,
∴![]() 是异面直线PC,BD所成的角,
是异面直线PC,BD所成的角,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面ABCD,
平面ABCD,
∴![]() ,
,![]() ,
,
![]() ,
,
∴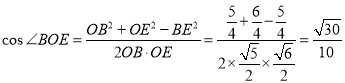 ,
,
∴![]() .
.
即异面直线PC与BD所成的角为![]() .
.
(2)P到平面ABCD的距离![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 或
或![]() .
.
(3)设![]() ,则
,则![]() ,折起后平面
,折起后平面![]() 平面AECD,
平面AECD,
则![]() 为直线
为直线![]() 与平面AECD所成的角.
与平面AECD所成的角.
于是![]() ,
,
要使![]() 最短,则
最短,则![]() 折起后应最小,
折起后应最小,![]() 最大,
最大,
∴当![]() 即
即![]() 时,
时,![]() 最大,
最大,
此时![]() 最短,
最短,
即当![]() 时,沿AE折起后
时,沿AE折起后![]() 间距离最短.
间距离最短.


科目:高中数学 来源: 题型:
【题目】(多选题)下列说法正确的是( )
A.椭圆![]() 1上任意一点(非左右顶点)与左右顶点连线的斜率乘积为
1上任意一点(非左右顶点)与左右顶点连线的斜率乘积为![]()
B.过双曲线![]() 1焦点的弦中最短弦长为
1焦点的弦中最短弦长为![]()
C.抛物线y2=2px上两点A(x1,y1).B(x2,y2),则弦AB经过抛物线焦点的充要条件为x1x2![]()
D.若直线与圆锥曲线有一个公共点,则该直线和圆锥曲线相切
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了选拔学生参加全市中学生物理竞赛,学校先从高三年级选取60名同学进行竞赛预选赛,将参加预选赛的学生成绩(单位:分)按范围![]() ,
,![]() ,
,![]() ,
,![]() 分组,得到的频率分布直方图如图:
分组,得到的频率分布直方图如图:

(1)计算这次预选赛的平均成绩(同一组中的数据用该组区间的中点值作代表);
(2)若对得分在前![]() 的学生进行校内奖励,估计获奖分数线;
的学生进行校内奖励,估计获奖分数线;
(3)若这60名学生中男女生比例为![]() ,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面
,成绩不低于60分评估为“成绩良好”,否则评估为“成绩一般”,试完成下面![]() 列联表,是否有
列联表,是否有![]() 的把握认为“成绩良好”与“性别”有关?
的把握认为“成绩良好”与“性别”有关?
成绩良好 | 成绩一般 | 合计 | |
男生 | |||
女生 | |||
合计 |
附:![]() ,
,![]()
临界值表:
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代数学名著《九章算术》中记载了有关特殊几何体的定义:阳马指底面为矩形,一侧棱垂直于底面的四棱锥,堑堵指底面是直角三角形,且侧棱垂直于底面的三棱柱.
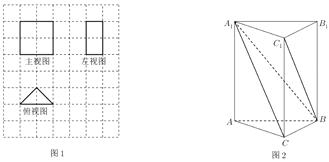
(1)某堑堵的三视图,如图1,网格中的每个小正方形的边长为1,求该堑堵的体积;
(2)在堑堵![]() 中,如图2,
中,如图2,![]() ,若
,若![]() ,当阳马
,当阳马![]() 的体积最大时,求二面角
的体积最大时,求二面角![]() 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某人打算做一个正四棱锥形的金字塔模型,先用木料搭边框,再用其他材料填充,已知金字塔的每一条棱和边都相等.
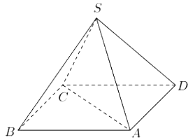
(1)求证:直线AC垂直于直线SD;
(2)若搭边框共使用木料24米,则需要多少立方米的填充材料才能将整个金字塔内部填满?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50名学生在一次百米测试中,成绩全部介于13秒与18秒之间,将测试结果按如下方式分成五组:第一组![]() ,第二组
,第二组![]() ,
,![]() ,第五组
,第五组![]() .下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.
.下图是按上述分组方法得到的频率分布直方图.按上述分组方法得到的频率分布直方图.

(1)若成绩大于或等于14秒且小于16秒认为良好,求该班在这次百米测试中成绩良好的人数;
(2)设m,n表示该班某两位同学的百米测试成绩,且已知![]() 求事件“
求事件“![]() ”发生的概率.
”发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() =1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
=1(a>0,b>0)的左、右焦点分别为F1,F2,点O为双曲线的中心,点P在双曲线右支上,△PF1F2内切圆的圆心为Q,圆Q与x轴相切于点A,过F2作直线PQ的垂线,垂足为B,则下列结论成立的是( )
A. |OA|>|OB|B. |OA|<|OB|
C. |OA|=|OB|D. |OA|与|OB|大小关系不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com