【题目】将高二（1）班的四个同学分到语文、数学、英语三个兴趣小组，每个兴趣小组至少有一名同学的分配方法有多少种？下列结论正确的有（ ）
A.
B.
C.
D.18
【答案】BC
【解析】
根据题意，有2种解法，
解法1，先将4人分三组，再将分好的三组全排列，由分布计数原理计算可得B正确；
解法2，在3个小组中选出1个，安排2个同学，再将剩下的2人全排列，对应剩下的2个兴趣小组，由分布计数原理计算可得C正确；即可得答案；
解：根据题意，
解法1，先将4人三组，有C42种分组方法，再将分好的三组全排列，对应三个兴趣小组，有A33种情况，则有C42A33种分配方法，B正确；
解法2，在3个小组中选出1个，安排2个同学，有C31C42种情况，再将剩下的2人全排列，对应剩下的2个兴趣小组，有A22种情况，则有C31C42A22种分配方法，C正确；
故选：BC.
阅读快车系列答案科目：高中数学 来源： 题型：
【题目】某医疗器械公司在全国共有
个销售点，总公司每年会根据每个销售点的年销量进行评价分析.规定每个销售点的年销售任务为一万四千台器械.根据这个销售点的年销量绘制出如下的频率分布直方图.
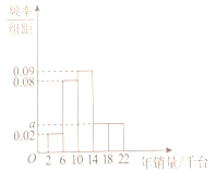
（1）完成年销售任务的销售点有多少个？
（2）若用分层抽样的方法从这个销售点中抽取容量为
的样本，求该五组
，
，
，
，
，（单位：千台）中每组分别应抽取的销售点数量.
（3）在（2）的条件下，从前两组，中的销售点随机选取
个，记这个销售点在中的个数为
，求的分布列和期望.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的两个焦点
，
，且椭圆过点
，
，且
是椭圆上位于第一象限的点，且
的面积
.
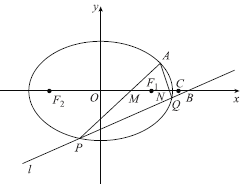
（1）求点的坐标；
（2）过点
的直线
与椭圆
相交于点
，
，直线
，
与
轴相交于
，
两点，点
，则
是否为定值，如果是定值，求出这个定值，如果不是请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】 据观测统计，某湿地公园某种珍稀鸟类的现有个数约
只，并以平均每年
的速度增加．
(1)求两年后这种珍稀鸟类的大约个数；
(2)写出
（珍稀鸟类的个数）关于
（经过的年数）的函数关系式；
(3)约经过多少年以后，这种鸟类的个数达到现有个数的
倍或以上？（结果为整数）(参考数据：
，
)
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知
，n∈N*.
（1）设f(x)＝a0+a1x+a2x2+…+anxn，
①求a0+a1+a2+…+an；
②若在a0，a1，a2，…，an中，唯一的最大的数是a4，试求n的值；
（2）设f(x)＝b0+b1(x+1)+b2(x+1)2+…+bn(x+1)n，求
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
