
【题目】设等差数列![]() 的首项为0,公差为a,
的首项为0,公差为a,![]() ;等差数列
;等差数列![]() 的首项为0,公差为b,
的首项为0,公差为b,![]() .由数列
.由数列![]() 和
和![]() 构造数表M,与数表
构造数表M,与数表![]() ;
;
记数表M中位于第i行第j列的元素为![]() ,其中
,其中![]() ,(i,j=1,2,3,…).
,(i,j=1,2,3,…).
记数表![]() 中位于第i行第j列的元素为
中位于第i行第j列的元素为![]() ,其中
,其中![]() (
(![]() ,
,![]() ,
,![]() ).如:
).如:![]() ,
,![]() .
.
(1)设![]() ,
,![]() ,请计算
,请计算![]() ,
,![]() ,
,![]() ;
;
(2)设![]() ,
,![]() ,试求
,试求![]() ,
,![]() 的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表
的表达式(用i,j表示),并证明:对于整数t,若t不属于数表M,则t属于数表![]() ;
;
(3)设![]() ,
,![]() ,对于整数t,t不属于数表M,求t的最大值.
,对于整数t,t不属于数表M,求t的最大值.
【答案】(1)![]() (2)详见解析(3)29
(2)详见解析(3)29
【解析】
(1)将![]() ,
,![]() 代入,可求出
代入,可求出![]() ,
,![]() ,可代入求
,可代入求![]() ,
,![]() ,可求结果.
,可求结果.
(2)可求![]() ,
,![]() ,通过反证法证明,
,通过反证法证明,
(3)可推出![]() ,
,![]() ,
,![]() 的最大值,就是集合
的最大值,就是集合![]() 中元素的最大值,求出.
中元素的最大值,求出.
(1)由题意知等差数列![]() 的通项公式为:
的通项公式为:![]() ;
;
等差数列![]() 的通项公式为:
的通项公式为:![]() ,
,
得![]() ,
,
则![]() ,
,![]() ,
,
得![]() ,
,
故![]() .
.
(2)证明:已知![]() .
.![]() ,由题意知等差数列
,由题意知等差数列![]() 的通项公式为:
的通项公式为:![]() ;
;
等差数列![]() 的通项公式为:
的通项公式为:![]() ,
,
得![]() ,
,![]() ,
,![]() .
.
得![]() ,
,![]() ,
,![]() ,
,![]() .
.
所以若![]() ,则存在
,则存在![]() ,
,![]() ,使
,使![]() ,
,
若![]() ,则存在
,则存在![]() ,
,![]() ,
,![]() ,使
,使![]() ,
,
因此,对于正整数![]() ,考虑集合
,考虑集合![]() ,
,![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
下面证明:集合![]() 中至少有一元素是7的倍数.
中至少有一元素是7的倍数.
反证法:假设集合![]() 中任何一个元素,都不是7的倍数,则集合
中任何一个元素,都不是7的倍数,则集合![]() 中每一元素关于7的余数可以为1,2,3,4,5,6,
中每一元素关于7的余数可以为1,2,3,4,5,6,
又因为集合![]() 中共有7个元素,所以集合
中共有7个元素,所以集合![]() 中至少存在两个元素关于7的余数相同,
中至少存在两个元素关于7的余数相同,
不妨设为![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() .则这两个元素的差为7的倍数,即
.则这两个元素的差为7的倍数,即![]() ,
,
所以![]() ,与
,与![]() 矛盾,所以假设不成立,即原命题成立.
矛盾,所以假设不成立,即原命题成立.
即集合![]() 中至少有一元素是7的倍数,不妨设该元素为
中至少有一元素是7的倍数,不妨设该元素为![]() ,
,![]() ,
,![]() ,
,
则存在![]() ,使
,使![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,![]() ,
,![]() ,
,
由已证可知,若![]() ,则存在
,则存在![]() ,
,![]() ,使
,使![]() ,而
,而![]() ,所以
,所以![]() 为负整数,
为负整数,
设![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以,当![]() ,
,![]() 时,对于整数
时,对于整数![]() ,若
,若![]() ,则
,则![]() 成立.
成立.
(3)下面用反证法证明:若对于整数![]() ,
,![]() ,则
,则![]() ,假设命题不成立,即
,假设命题不成立,即![]() ,且
,且![]() .
.
则对于整数![]() ,存在
,存在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,使
,使![]() 成立,
成立,
整理,得![]() ,
,
又因为![]() ,
,![]() ,
,
所以![]() 且
且![]() 是7的倍数,
是7的倍数,
因为![]() ,
,![]() ,所以
,所以![]() ,所以矛盾,即假设不成立.
,所以矛盾,即假设不成立.
所以对于整数![]() ,若
,若![]() ,则
,则![]() ,
,
又由第二问,对于整数![]() ,则
,则![]() ,
,
所以![]() 的最大值,就是集合
的最大值,就是集合![]() 中元素的最大值,
中元素的最大值,
又因为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.


科目:高中数学 来源: 题型:
【题目】设函数f(x)=ax2–a–lnx,g(x)=![]() ,其中a∈R,e=2.718…为自然对数的底数.
,其中a∈R,e=2.718…为自然对数的底数.
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)证明:当x>1时,g(x)>0;
(Ⅲ)确定a的所有可能取值,使得f(x)>g(x)在区间(1,+∞)内恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
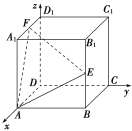
【题目】如图,在正方体ABCD![]() 中,以D为原点建立空间直角坐标系,E为B
中,以D为原点建立空间直角坐标系,E为B![]() 的中点,F为
的中点,F为![]() 的中点,则下列向量中,能作为平面AEF的法向量的是( )
的中点,则下列向量中,能作为平面AEF的法向量的是( )
A. (1,-2,4) B. (-4,1,-2)
C. (2,-2,1) D. (1,2,-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式mx2-2x-m+1<0对于满足|m|≤2的一切m的值都成立,求x的取值范围.
【答案】![]()
【解析】
令f(m)=m(x2﹣1)﹣2x+1,由条件f(m)<0对满足|m|≤2的一切m的值都成立,利用一次函数的单调性可得:f(﹣2)<0,f(2)<0.解出即可.
令f(m)=m(x2﹣1)﹣2x+1,由条件f(m)<0对满足|m|≤2的一切m的值都成立,
则需要f(﹣2)<0,f(2)<0.
解不等式组![]() ,解得
,解得![]() ,
,
∴x的取值范围是![]() .
.
【点睛】
本题考查了一次函数的单调性、一元二次不等式的解法,考查了转化方法,考查了推理能力与计算能力,属于中档题.
【题型】解答题
【结束】
21
【题目】某厂有一批长为18m的条形钢板,可以割成1.8m和1.5m长的零件.它们的加工费分别为每个1元和0.6元.售价分别为20元和15元,总加工费要求不超过8元.问如何下料能获得最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从高三年级期末考试的学生中抽出60名学生,其成绩(均为整数)的频率分布直方图如图所示:
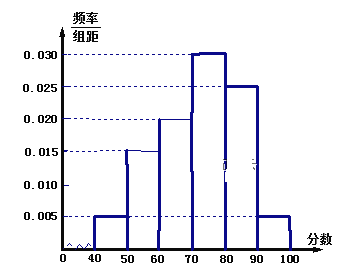
(1)估计这次考试的及格率(60分及以上为及格)和平均分;
(2)按分层抽样从成绩是80分以上(包括80分)的学生中选取6人,再从这6人中选取两人作为代表参加交流活动,求他们在不同分数段的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)3个不同的球放入5个不同的盒子,每个盒子至多放1个球,共有多少种放法?
(2)3个不同的球放入5个不同的盒子,每个盒子放球量不限,共有多少种放法?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com