
【题目】如图,矩形ABCD所在的平面和平面![]() 互相垂直,等腰梯形
互相垂直,等腰梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分别为
分别为![]() 的中点,
的中点, ![]() 为底面
为底面![]() 的重心.
的重心.
(Ⅰ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
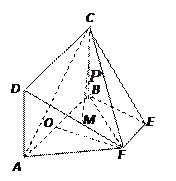
【答案】(1)见解析(2) ![]()
【解析】试题分析:(1)根据重心定义,可得连结![]() 延长交
延长交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点,根据三角形中位线性质得
的中点,根据三角形中位线性质得![]() ∥
∥![]() ,再由线面平行判定定理得
,再由线面平行判定定理得![]() ∥平面
∥平面![]() ,同理可得
,同理可得![]() ∥平面
∥平面![]() ,因此平面
,因此平面![]() ∥平面
∥平面![]() ,即得
,即得![]() ∥平面
∥平面![]() ;(2)利用面面垂直性质定理寻找线面垂直:作AQ⊥EF,则得AQ⊥平面ABCD,作AH⊥DQ,可得AH⊥面EQDC,因此直线
;(2)利用面面垂直性质定理寻找线面垂直:作AQ⊥EF,则得AQ⊥平面ABCD,作AH⊥DQ,可得AH⊥面EQDC,因此直线![]() 与平面
与平面![]() 所成角为∠ACH,解直角三角形得直线AC与平面CEF所成角正弦值
所成角为∠ACH,解直角三角形得直线AC与平面CEF所成角正弦值
试题解析:(Ⅰ)连结![]() 延长交
延长交![]() 于
于![]() ,则
,则![]() 为
为![]() 的中点,又
的中点,又![]() 为
为![]() 的中点,
的中点,
∴![]() ∥
∥![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]()
连结![]() ,则
,则![]() ∥
∥![]() ,
, ![]() 平面
平面![]() ,∴
,∴![]() ∥平面
∥平面![]()
![]() ∴平面
∴平面![]() ∥平面
∥平面![]() ,
, ![]() 平面
平面![]()
![]()
![]() 平面
平面![]()
(Ⅱ)作AQ⊥EF交EF延长线于Q,作AH⊥DQ交DQ于H,则AH⊥面EQDC
∴∠ACH就是直线AC与平面CEF所成角
在Rt![]() ADQ中,AH=
ADQ中,AH=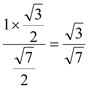
在Rt![]() ACH中,sin∠ACH=
ACH中,sin∠ACH=![]()
直线AC与平面CEF所成角正弦值为![]()


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=x2﹣16x+q+3:
(1)若函数在区间[﹣1,1]上存在零点,求实数q的取值范围;
(2)问:是否存在常数t(t≥0),当x∈[t,10]时,f(x)的值域为区间D,且D的长度为12﹣t.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣2x2+ax+b且f(2)=﹣3.
(1)若函数f(x)的图象关于直线x=1对称,求函数f(x)在区间[﹣2,3]上的值域;
(2)若函数f(x)在区间[1,+∞)上递减,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设二次函数f(x)=ax2+bx+c(a≠0)在区间[﹣2,2]上的最大值、最小值分别是M,m,集合A={x|f(x)=x}.
(1)若A={1,2},且f(0)=2,求M和m的值;
(2)若A={1},且a≥1,记g(a)=M+m,求g(a)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)为定义在R上的奇函数,且当x>0时,f(x)=1﹣x2 .
(1)求函数f(x)的解析式;
(2)作出函数f(x)的图象.
(3)若函数f(x)在区间[a,a+1]上单调,直接写出实数a的取值范围.(不必写出演算过程)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣4,4)、B(4,4),直线AM与BM相交于点M,且直线AM的斜率与直线BM的斜率之差为﹣2,点M的轨迹为曲线C.
(1)求曲线C 的轨迹方程;
(2)Q为直线y=﹣1上的动点,过Q做曲线C的切线,切点分别为D、E,求△QDE的面积S的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在高中学习过程中,同学们经常这样说:“数学物理不分家,如果物理成绩好,那么学习数学就没什么问题.”某班针对“高中生物理学习对数学学习的影响”进行研究,得到了学生的物理成绩与数学成绩具有线性相关关系的结论,现从该班随机抽取5名学生在一次考试中的数学和物理成绩,如下表:
编号 成绩 | 1 | 2 | 3 | 4 | 5 |
物理( | 90 | 85 | 74 | 68 | 63 |
数学( | 130 | 125 | 110 | 95 | 90 |
(1)求数学成绩![]() 对物理成绩
对物理成绩![]() 的线性回归方程
的线性回归方程![]() (
(![]() 精确到
精确到![]() ),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
),若某位学生的物理成绩为80分,预测他的数学成绩(结果精确到个位);
(2)要从抽取的这五位学生中随机选出2位参加一项知识竞赛,求选中的学生的数学成绩至少有一位高于120分的概率.
(参考公式: 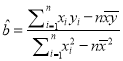 ,
, ![]() .)
.)
(参考数据: ![]() ,
, ![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在“出彩中国人”的一期比赛中,有6位歌手(1~6)登台演出,由现场的百家大众媒体投票选出最受欢迎的出彩之星,各家媒体独立地在投票器上选出3位出彩候选人,其中媒体甲是1号歌手的歌迷,他必选1号,另在2号至6号中随机的选2名;媒体乙不欣赏2号歌手,他必不选2号;媒体丙对6位歌手的演唱没有偏爱,因此在1至6号歌手中随机的选出3名.
(1)求媒体甲选中3号且媒体乙未选中3号歌手的概率;
(2)X表示3号歌手得到媒体甲、乙、丙的票数之和,求X的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com