
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取![]() 名工人,将他们随机分成两组,每组
名工人,将他们随机分成两组,每组![]() 人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:
人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:![]() )绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
)绘制了如图所示的茎叶图(茎为十位数,叶为个位数):
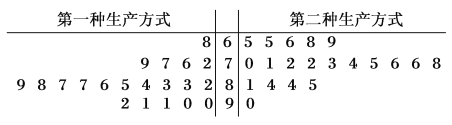
(1)根据茎叶图,估计两种生产方式完成任务所需时间至少![]() 分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
分钟的概率,并对比两种生产方式所求概率,判断哪种生产方式的效率更高?
(2)将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的工人数填入下面的列联表:
的工人数填入下面的列联表:
超过 | 不超过 | |
第一种生产方式 | ||
第二种生产方式 |
(3)根据(2)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: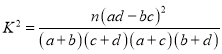
|
|
|
|
|
|
|
|
【答案】(1)第一种和第二生产方式完成任务所需时间至少![]() 分钟的概率分别为
分钟的概率分别为![]() 、
、![]() ,第二种生产方式的效率更高;(2)列联表见解析;(3)没有.
,第二种生产方式的效率更高;(2)列联表见解析;(3)没有.
【解析】
(1)根据茎叶图中的数据分别计算出用第一种和第二种生产方式完成任务所需时间至少![]() 分钟的概率,比较大小后可得出结论;
分钟的概率,比较大小后可得出结论;
(2)根据茎叶图中的数据可完善列联表;
(3)根据列联表中的数据计算出观测值,对照临界值得出结论.
(1)用第一种生产方式的工人中,完成生产任务所需时间至少![]() 分钟的概率为
分钟的概率为![]() ,
,
用第二种生产方式的工人中,完成生产任务所需时间至少![]() 分钟的概率为
分钟的概率为![]() ,
,
因为![]() ,所以第二种生产方式时间更短,因此第二种生产方式的效率更高;
,所以第二种生产方式时间更短,因此第二种生产方式的效率更高;
(2)列联表如下:
超过 | 不超过 | |
第一种生产方式 |
|
|
第二种生产方式 |
|
|
(3)由于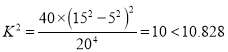 ,所以没有
,所以没有![]() 的把握认为两种生产方式的效率有差异.
的把握认为两种生产方式的效率有差异.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:
【题目】某房地产公司新建小区有A、B两种户型住宅,其中A户型住宅每套面积为100平方米,B户型住宅每套面积为80平方米,该公司准备从两种户型住宅中各拿出12套销售给内部员工,表是这24套住宅每平方米的销售价格:(单位:万元平方米):
房号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A户型 | 2.6 | 2.7 | 2.8 | 2.8 | 2.9 | 3.2 | 2.9 | 3.1 | 3.4 | 3.3 | 3.4 | 3.5 |
B户型 | 3.6 | 3.7 | 3.7 | 3.9 | 3.8 | 3.9 | 4.2 | 4.1 | 4.1 | 4.2 | 4.3 | 4.5 |
(1)根据表格数据,完成下列茎叶图,并分别求出A,B两类户型住宅每平方米销售价格的中位数;
A户型 | B户型 | |
2. | ||
3. | ||
4. |
(2)该公司决定对上述24套住房通过抽签方式销售,购房者根据自己的需求只能在其中一种户型中通过抽签方式随机获取房号,每位购房者只有一次抽签机会,小明是第一位抽签的员工,经测算其购买能力最多为320万元,抽签后所抽得住房价格在其购买能力范围内则确定购买,否则,将放弃此次购房资格,为了使其购房成功的概率更大,他应该选择哪一种户型抽签?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1,F2为椭圆E:![]() 的左、右焦点,且|F1F2|=2
的左、右焦点,且|F1F2|=2![]() ,点
,点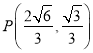 在E上.
在E上.
(1)求E的方程;
(2)直线l与以E的短轴为直径的圆相切,l与E交于A,B两点,O为坐标原点,试判断O与以AB为直径的圆的位置关系,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a、b、c分别是角A、B、C的对边,向量![]() =(2sinB,2-cos2B),
=(2sinB,2-cos2B),![]() =(2sin2(
=(2sin2(![]() ),-1),
),-1),![]() .
.
(1)求角B的大小;
(2)若a=![]() ,b=1,求c的值.
,b=1,求c的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]()
![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设s,t是不相等的两个正数,且s+slnt=t+tlns,则s+t﹣st的取值范围为( )
A.(﹣∞,1)B.(﹣∞,0)C.(0,+∞)D.(1,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() ,过焦点
,过焦点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() ,
,![]() 两点,且当直线
两点,且当直线![]() 倾斜角为
倾斜角为![]() 时,与抛物线相交所得弦的长度为8.
时,与抛物线相交所得弦的长度为8.
(1)求抛物线![]() 的方程;
的方程;
(2)若分别过点![]() ,
,![]() 两点作抛物线
两点作抛物线![]() 的切线
的切线![]() ,
,![]() ,两条切线相交于点
,两条切线相交于点![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,判断四边形
,判断四边形![]() 是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
是否存在外接圆,如果存在,求出外接圆面积的最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型商场的空调在1月到5月的销售量与月份相关,得到的统计数据如下表:
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
(1)经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量![]() (百件)与月份
(百件)与月份![]() 之间的相关关系.请用最小二乘法求
之间的相关关系.请用最小二乘法求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并预测6月份该商场空调的销售量;
,并预测6月份该商场空调的销售量;
(2)若该商场的营销部对空调进行新一轮促销,对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大,经过营销部调研机构对其中的500名顾客进行了一个抽样调查,得到如下一份频数表:
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名,再从这6人中随机抽取3人进行跟踪调查,求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据:线性回归方程![]() ,其中
,其中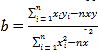 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com