
【题目】已知二次函数g(x)=mx2﹣2mx+n+1(m>0)在区间[0,3]上有最大值4,最小值0.
(1)求函数g(x)的解析式;
(2)设f(x)= ![]() .若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
.若f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,求k的取值范围.
【答案】
(1)解:∵g(x)=m(x﹣1)2﹣m+1+n
∴函数g(x)的图象的对称轴方程为x=1
∵m>0依题意得 ![]() ,
,
即 ![]() ,
,
解得 ![]()
∴g(x)=x2﹣2x+1,
(2)解:∵ ![]()
∴ ![]() ,
,
∵f(2x)﹣k2x≤0在x∈[﹣3,3]时恒成立,
即 ![]() 在x∈[﹣3,3]时恒成立
在x∈[﹣3,3]时恒成立
∴ ![]() 在x∈[﹣3,3]时恒成立
在x∈[﹣3,3]时恒成立
只需 ![]()
令 ![]() ,
,
由x∈[﹣3,3]得 ![]()
设h(t)=t2﹣4t+1
∵h(t)=t2﹣4t+1
=(t﹣2)2﹣3
∴函数h(x)的图象的对称轴方程为t=2
当t=8时,取得最大值33.
∴k≥h(t)max=h(8)=33
∴k的取值范围为[33,+∞)
【解析】(1)由题意得方程组解出即可,(2)将f(x)进行变形,通过换元求出函数h(t)的最值,从而求出k的值.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】如表提供了甲产品的产量x(吨)与利润y(万元)的几组对照数据.
x | 3 | 4 | 5 | 6 |
y | 2.5 | 3 | 4 | 4.5 |
(1)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 ![]() =
= ![]() x+
x+ ![]() ;
;
(2)计算相关指数R2的值,并判断线性模型拟合的效果.
参考公式: ![]() =
= 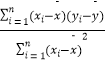 =
= 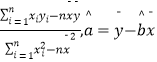 ,R2=1﹣
,R2=1﹣ 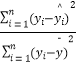 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣2|+|x﹣a|.
(1)当a=2时,求不等式f(x)≥4的解集;
(2)不等式f(x)<4的解集中的整数有且仅有1,2,3,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图的程序框图表示求式子1×3×7×15×31×63的值,则判断框内可以填的条件为( ) 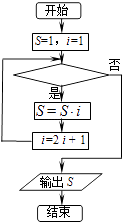
A.i≤31?
B.i≤63?
C.i≥63?
D.i≤127?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() 底面
底面![]() ,
, ![]() 是棱
是棱![]() 的中点,
的中点,
且![]() .
.

(1)求证: ![]() 平面
平面![]() ;
;
(2)如果![]() 是棱
是棱![]() 上一点,且直线
上一点,且直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数f(x)=kax﹣a﹣x(a>0且a≠1)在(﹣∞,+∞)上既是奇函数又是增函数,则函数g(x)=loga(x+k)的图象是( )
A.
B.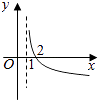
C.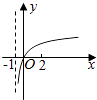
D.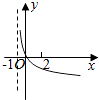
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的焦点在抛物线
的焦点在抛物线![]() 上,点
上,点![]() 是抛物线
是抛物线![]() 上的动点.
上的动点.
(Ⅰ)求抛物线![]() 的方程及其准线方程;
的方程及其准线方程;
(Ⅱ)过点![]() 作抛物线
作抛物线![]() 的两条切线,
的两条切线, ![]() 、
、![]() 分别为两个切点,求
分别为两个切点,求![]() 面积的最小值.
面积的最小值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com