
分析 (1)由题意设t=$\sqrt{1-2x}$,求出t的范围和x的表达式,代入f(x)化简后,根据一元二次函数的性质和t的范围,求出函数f(x)的值域;
(2)令x取$\frac{1}{x}$代入原方程化简,与原方程联立后求出f(x)的解析式.
解答 解:(1)设t=$\sqrt{1-2x}$,则t≥0,x=$\frac{1-{t}^{2}}{2}$,
代入f(x)得,y=$\frac{1-{t}^{2}}{2}$+t=$-\frac{1}{2}(t-1)^{2}+1$,
因为t≥0,所以函数y的最大值是1,
即函数f(x)的值域是[1,+∞);
(2)由题意得,$f(x)+2f(\frac{1}{x})=3x-2$,①
令x取$\frac{1}{x}$代入得,$f(\frac{1}{x})+2f(x)=\frac{3}{x}-2$,②
由①②解得f(x)=$\frac{2}{x}-x-\frac{2}{3}$.
点评 本题考查换元法求函数的值域,列方程法求函数的解析式,以及一元二次函数的性质,属于中档题.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源: 题型:解答题
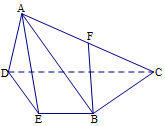 如图,在空间几何体A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.
如图,在空间几何体A-BCDE中,底面BCDE是梯形,且CD∥BE,CD=2BE=4,∠CDE=60°,△ADE是边长为2的等边三角形,F为AC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{20}$=1 | B. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{5}$=1 | C. | $\frac{{x}^{2}}{25}$-$\frac{{y}^{2}}{20}$=1 | D. | $\frac{{x}^{2}}{20}$-$\frac{{y}^{2}}{25}$=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 患呼吸系统疾病 | 未患呼吸系统疾病 | 总计 | |
| 重污染地区 | 103 | 1 397 | 1 500 |
| 轻污染地区 | 13 | 1 487 | 1 500 |
| 总计 | 116 | 2 884 | 3 000 |
| P(K2≥k0) | 0.010 | 0.005 | 0.001 |
| k0 | 6.635 | 7.879 | 10828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com