已知函数y=f(x)满足f(a-tanθ)=cotθ-1,(其中,a、θ∈R均为常数)
(1)求函数y=f(x)的解析式;
(2)利用函数y=f(x)构造一个数列{xn},方法如下:
对于给定的定义域中的x1,令x2=f(x1),x3=f(x2),…,xn=f(xn-1),…
在上述构造过程中,如果xi(i=1,2,3,…)在定义域中,构造数列的过程继续下去;如果xi不在定义域中,则构造数列的过程停止.
①如果可以用上述方法构造出一个常数列{xn},求a的取值范围;
②如果取定义域中的任一值作为x1,都可以用上述方法构造出一个无穷数列{xn},求a实数的值.
解:(1)令

,则
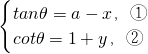
①×②,并整理,得y=
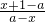
,
∴y=f(x)=
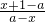
,(x≠a).(4分)
(2)①根据题意,只需当x≠a时,方程f(x)=x有解,
亦即方程x
2+(1-a)x+1-a=0有不等于a的解.
将x=a代入方程左边,得左边为1,故方程不可能有解x=a.
由△=(1-a)
2-4(1-a)≥0,得a≤-3或a≥1,
即实数a的取值范围是(-∞,3]∪[1,+∞).(9分)
②根据题意,
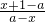
=a在R中无解,
亦即当x≠a时,方程(1+a)x=a
2+a-1无实数解.
由于x=a不是方程(1+a)x=a
2+a-1的解,
所以对于任意x∈R,方程(1+a)x=a
2+a-1无实数解,
∴a=-1即为所求a的值.(14分)
分析:(1)由

,可推导出y=f(x)=
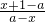
,(x≠a).
(2)①根据题意,只需当x≠a时,方程f(x)=x有解,方程x
2+(1-a)x+1-a=0有不等于a的解.将x=a代入方程左边,得左边为1,故方程不可能有解x=a.由由根的判别式,可得a的取值范围是(-∞,3]∪[1,+∞).
②根据题意,
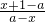
=a在R中无解,亦即当x≠a时,方程(1+a)x=a
2+a-1无实数解.由此能够导出a=-1.
点评:本题考查函数的性质和应用,解题时要认真审题,仔细解答.

 ,则
,则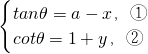
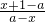 ,
,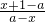 ,(x≠a).(4分)
,(x≠a).(4分)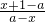 =a在R中无解,
=a在R中无解, ,可推导出y=f(x)=
,可推导出y=f(x)=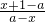 ,(x≠a).
,(x≠a).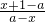 =a在R中无解,亦即当x≠a时,方程(1+a)x=a2+a-1无实数解.由此能够导出a=-1.
=a在R中无解,亦即当x≠a时,方程(1+a)x=a2+a-1无实数解.由此能够导出a=-1.

 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为