Question

【题目】如下图，在空间多面体中，四边形为直角梯形，， ，是正三角形，，。

（Ⅰ）求证：平面平面；

（Ⅱ）求二面角的余弦值。

Answer 1

【答案】（Ⅰ）证明见解析；（Ⅱ）。

【解析】

试题分析：（Ⅰ）借助题设条件运用面面垂直的判定定理推证；（Ⅱ）借助题设条件运用二面角的定义进行转化为平面角或运用空间向量的数量积公式求解。

试题解析：

证明：（Ⅰ）因为，，

所以，

所以,

因为,

所以平面，

因为平面，

所以平面平面，

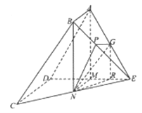
法一：（Ⅱ）取中点，连接，过作，过作，连接，所以是二面角的平面角，

设，

在中，，所以，

在中，，所以，，

因为，所以，

在中，所以，

因为，所以,

所以，

过作，则是中点，

所以，

在中，，

所以，即二面角的余弦值为。

法二：（Ⅱ）过作，过作，，

连接，则是正方形，

因为，所以，

所以是梯形，

过作，连接，

因为，平面，

所以，即，

则是二面角的平面角，

设，则，

在，，,

所以，，

所以，

所以二面角的余弦值为。

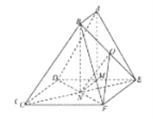
法三：（Ⅲ）过点作平面，由（Ⅰ）知：平面平面，所以平面，

以为原点，分别以为轴、轴、轴建立空间直角坐标系，则，，，因为，且，所以，

，，，，

设平面的法向量为，则，

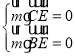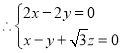，取，

同理可得平面的法向量，

所以，

因为二面角是钝角，所以其余弦值是。