
【题目】在平面直角坐标系![]() 中,已知圆
中,已知圆![]() ,椭圆
,椭圆![]() ,
, ![]() 为椭圆
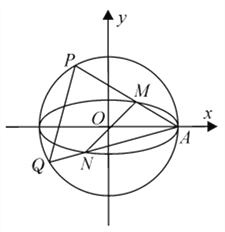
为椭圆![]() 的右顶点,过原点且异于
的右顶点,过原点且异于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 交于
交于![]() 两点,
两点, ![]() 在
在![]() 轴的上方,直线
轴的上方,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,直线
,直线![]() 与圆
与圆![]() 的另一交点为
的另一交点为![]() ,
,
(1)若![]() ,求直线
,求直线![]() 的斜率;
的斜率;
(2)设![]() 与
与![]() 的面积分别为
的面积分别为![]() ,求
,求![]() 的最大值.
的最大值.
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】已知向量 ![]() =(cos
=(cos ![]() ,sin
,sin ![]() ),
), ![]() =(cos
=(cos ![]() ,﹣sin
,﹣sin ![]() ),函数f(x)=
),函数f(x)= ![]()
![]() ﹣m|
﹣m| ![]() +
+ ![]() |+1,x∈[﹣
|+1,x∈[﹣ ![]() ,
, ![]() ],m∈R.
],m∈R.
(1)当m=0时,求f( ![]() )的值;
)的值;
(2)若f(x)的最小值为﹣1,求实数m的值;
(3)是否存在实数m,使函数g(x)=f(x)+ ![]() m2 , x∈[﹣
m2 , x∈[﹣ ![]() ,
, ![]() ]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
]有四个不同的零点?若存在,求出m的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数 ![]() ,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
,x∈R的图象,只需把函数y=2sinx,x∈R的图象上所有的点( )
A.向左平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍纵坐标不变)
倍纵坐标不变)
B.向右平移 ![]() 个单位长度,再把所得各点的横坐标缩短到原来的
个单位长度,再把所得各点的横坐标缩短到原来的 ![]() 倍(纵坐标不变)
倍(纵坐标不变)
C.向左平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
D.向右平移 ![]() 个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把所得各点的横坐标伸长到原来的3倍(纵坐标不变)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n∈N)的函数解析式.
(2)花店记录了100天玫瑰花的日需求量(单位:枝),整理得下表:
日需求量n | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数 | 10 | 20 | 16 | 16 | 15 | 13 | 10 |
以100天记录的各需求量的频率作为各需求量发生的概率.
(i)若花店一天购进16枝玫瑰花,X表示当天的利润(单位:元),求X的分布列,数学期望及方差;
(ii)若花店计划一天购进16枝或17枝玫瑰花,你认为应购进16枝还是17枝?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=lnx,g(x)= ![]() +mx+
+mx+ ![]() (m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(m<0),直线l与函数f(x)的图象相切,切点的横坐标为1,且直线l与函数g(x)的图象也相切.
(1)求直线l的方程及实数m的值;
(2)若h(x)=f(x+1)﹣g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的最大值;
(3)当0<b<a时,求证:f(a+b)﹣f(2a)< ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=( ![]() +
+ ![]() )x3(a>0,a≠1).
)x3(a>0,a≠1).
(1)讨论函数f(x)的奇偶性;
(2)求a的取值范围,使f(x)+f(2x)>0在其定义域上恒成立.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2 ![]() ﹣3(ω>0)
﹣3(ω>0)
(1)若 ![]() 是最小正周期为π的偶函数,求ω和θ的值;
是最小正周期为π的偶函数,求ω和θ的值;
(2)若g(x)=f(3x)在 ![]() 上是增函数,求ω的最大值.
上是增函数,求ω的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com