
【题目】某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(第![]() 周)和市场占有率(
周)和市场占有率(![]() )的几组相关数据如下表:
)的几组相关数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)根据表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)根据上述线性回归方程,预测在第几周,该款旗舰机型市场占有率将首次超过![]() (最后结果精确到整数).
(最后结果精确到整数).
参考公式: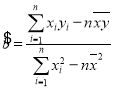 ,
,![]() .
.
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:高中数学 来源: 题型:
【题目】超市为了防止转基因产品影响民众的身体健康,要求产品在进入超市前必须进行两轮转基因检测,只有两轮都合格才能销售,否则不能销售.已知某产品第一轮检测不合格的概率为![]() ,第二轮检测不合格的概率为
,第二轮检测不合格的概率为![]() ,两轮检测是否合格相互没有影响.
,两轮检测是否合格相互没有影响.
(1)求该产品不能销售的概率;
(2)如果产品可以销售,则每件产品可获利50元;如果产品不能销售,则每件产品亏损60元.已知一箱中有产品4件,记一箱产品获利![]() 元,求
元,求![]() 的分布列,并求出均值
的分布列,并求出均值![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是正方形,点
是正方形,点![]() 在以
在以![]() 为直径的半圆弧上(
为直径的半圆弧上(![]() 不与
不与![]() ,
,![]() 重合),
重合),![]() 为线段
为线段![]() 的中点,现将正方形
的中点,现将正方形![]() 沿
沿![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() .
.

(1)证明:![]() 平面
平面![]() .
.
(2)若![]() ,当三棱锥
,当三棱锥![]() 的体积最大时,求
的体积最大时,求![]() 到平面
到平面![]() 的距离.
的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]:在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() ,
,![]() 的直角坐标方程;
的直角坐标方程;
(2)判断曲线![]() ,
,![]() 是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
是否相交,若相交,请求出交点间的距离;若不相交,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A、B、C的对边分别为a、b、c,且![]() .
.
(1)求角A;
(2)若△ABC外接圆的面积为4π,且△ABC的面积![]() ,求△ABC的周长.
,求△ABC的周长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】你知道吗,生产甲流H1N1流感疫苗的最主要原材料居然是鸡蛋!不过这可不是一种普通的鸡蛋,而是一种原产于美国的海兰白鸡蛋.工人们首先在强光照射下,挑选出“受过精”的鸡蛋,未“受过精”的鸡蛋只能作为普通食用蛋走上市场,这个过程叫做“照检”照检挑选出来的鸡蛋被送到疫苗生产车间,先经过严格的消毒,然后这些鸡蛋里面被植入由世卫组织提供的甲流毒株,这些接受了毒株的鸡蛋将被放置在特殊环境的车间里,使得毒株在鸡蛋里迅速生长,大约3天后,就“成熟”了.这时鸡蛋转到另一车间进行毒株的“收获”.鸡蛋里的羊水是我们需要的所谓的“病毒收获液”,剩下的蛋壳和未发育完整的小鸡将被高温消毒后送到其他企业,制成饲料.病毒收获液里含有我们需要的抗病毒成分,再依次经过了灭活、纯化、裂解后,就得到了我们需要的甲流疫苗了.下面是以上整个生产过程的流程图,则图中的①②位置上应分别填上( )
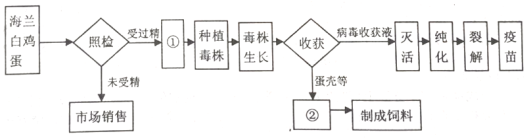
A.消毒、消毒B.挑选、消毒C.消毒、裂解D.消毒、挑选
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 相邻两对称轴间的距离为
相邻两对称轴间的距离为![]() ,若将
,若将![]() 的图象先向左平移
的图象先向左平移![]() 个单位,再向下平移1个单位,所得的函数
个单位,再向下平移1个单位,所得的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式,并求
的解析式,并求![]() 的对称中心;
的对称中心;
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不相等的实根,求实数
上有两个不相等的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】排成一排的10名学生生日的月份均不相同.有![]() 名教师,依次挑选这些学生参加
名教师,依次挑选这些学生参加![]() 个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求
个兴趣小组,每名学生恰被一名教师挑选,且保持学生的排序不变,每名教师挑出的学生必须满足生日的月份是逐渐增加或逐渐减少的(挑选一名或两名学生也认为是逐渐增加或逐渐减少的),每名教师尽可能多地选学生.对于学生所有可能的排序,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com