
【题目】已知椭圆的中心在坐标原点![]() ,焦点在
,焦点在![]() 轴上,短轴长为
轴上,短轴长为![]() ,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点
,且两个焦点和短轴的两个端点恰为一个正方形的顶点,过右焦点![]() 与
与![]() 轴不垂直的直线交椭圆于
轴不垂直的直线交椭圆于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆的方程.
(Ⅱ)当直线![]() 的斜率为
的斜率为![]() 时,求
时,求![]() 的面积.
的面积.
(Ⅲ)在线段![]() 上是否存在点
上是否存在点![]() ,使得经
,使得经![]() ,
, ![]() 为领边的平行四边形是菱形?若存在,求出
为领边的平行四边形是菱形?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)
;(Ⅱ) ![]() ;(Ⅲ)答案见解析.
;(Ⅲ)答案见解析.
【解析】试题分析:(1)由短轴长为![]() 得
得![]() ,由两个焦点和短轴的两个端点恰为一个正方形的顶点得
,由两个焦点和短轴的两个端点恰为一个正方形的顶点得![]() ,由此求出
,由此求出![]() ,即可求出椭圆方程;(2)先写出直线
,即可求出椭圆方程;(2)先写出直线![]() 的方程,将直线方程与椭圆方程联立,求出
的方程,将直线方程与椭圆方程联立,求出![]() 的坐标,从而求出
的坐标,从而求出![]() ,由点到直线的距离公式求出点
,由点到直线的距离公式求出点![]() 到到直线的距离即可求三角形的面积;(3) 设在线段
到到直线的距离即可求三角形的面积;(3) 设在线段![]() 上存在点
上存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形,设出直线方程
为邻边的平行四边形是菱形,设出直线方程![]() ,与椭圆方程联立,由韦达定理计算
,与椭圆方程联立,由韦达定理计算![]() ,即可求出
,即可求出![]() 的取值范围.
的取值范围.
试题解析:(1)设椭圆方程为![]()
![]() ,
,
根据题意得![]() 所以
所以![]() ,
,
所以椭圆方程为![]() ;
;
(2)根据题意得直线方程为![]() ,
,
解方程组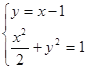 得
得![]() 坐标为
坐标为![]() , 计算
, 计算![]() ,
,
点![]() 到直线
到直线![]() 的距离为
的距离为![]() , 所以,
, 所以,![]() ;
;
(3)假设在线段![]() 上存在点
上存在点![]() ,使得以
,使得以![]() 为邻边的平行四边形是菱形.因为直线与
为邻边的平行四边形是菱形.因为直线与![]() 轴不垂直,所以设直线
轴不垂直,所以设直线![]() 的方程为
的方程为![]() .
.
![]() 坐标为
坐标为![]() ,
,![]()
由 得,
得,![]() ,
,
![]() ,
,
计算得:![]()
![]() ,其中
,其中![]() ,
,
由于以![]() 为邻边的平行四边形是菱形,所以
为邻边的平行四边形是菱形,所以![]() ,
,
计算得![]() , 即
, 即![]()
![]() ,
,![]() , 所以
, 所以![]() .
.
(可以设点,也可以设直线得到![]() 和
和![]() 的函数关系式)
的函数关系式)


科目:高中数学 来源: 题型:
【题目】若函数![]() 在
在![]() 上存在唯一的
上存在唯一的![]() 满足
满足![]() , 那么称函数
, 那么称函数![]() 是
是![]() 上的“单值函数”.已知函数
上的“单值函数”.已知函数![]() 是
是![]() 上的“单值函数”,当实数
上的“单值函数”,当实数![]() 取最小值时,函数
取最小值时,函数![]() 在
在![]() 上恰好有两点零点,则实数
上恰好有两点零点,则实数![]() 的取值范围是___________.
的取值范围是___________.
查看答案和解析>>
科目:高中数学 来源: 题型:
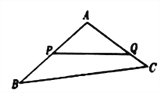
【题目】如图,某生态园将一块三角形地![]() 的一角
的一角![]() 开辟为水果园,已知角
开辟为水果园,已知角![]() 为
为![]() ,
, ![]() 的长度均大于200米,现在边界
的长度均大于200米,现在边界![]() 处建围墙,在
处建围墙,在![]() 处围竹篱笆.
处围竹篱笆.
(1)若围墙![]() 、
、![]() 总长度为200米,如何可使得三角形地块
总长度为200米,如何可使得三角形地块![]() 面积最大?
面积最大?
(2)已知竹篱笆长为![]() 米,
米, ![]() 段围墙高1米,
段围墙高1米, ![]() 段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
段围墙高2米,造价均为每平方米100元,求围墙总造价的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在曲线
在曲线![]() 上,⊙
上,⊙![]() 过原点
过原点![]() ,且与
,且与![]() 轴的另一个交点为
轴的另一个交点为![]() ,若线段
,若线段![]() ,⊙
,⊙![]() 和曲线
和曲线![]() 上分别存在点
上分别存在点![]() 、点
、点![]() 和点
和点![]() ,使得四边形
,使得四边形![]() (点
(点![]() ,
, ![]() ,
, ![]() ,
, ![]() 顺时针排列)是正方形,则称点
顺时针排列)是正方形,则称点![]() 为曲线
为曲线![]() 的“完美点”.那么下列结论中正确的是( ).
的“完美点”.那么下列结论中正确的是( ).
A. 曲线![]() 上不存在”完美点”
上不存在”完美点”
B. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]()
C. 曲线![]() 上只存在一个“完美点”,其横坐标大于
上只存在一个“完美点”,其横坐标大于![]() 且小于
且小于![]()
D. 曲线![]() 上存在两个“完美点”,其横坐标均大于
上存在两个“完美点”,其横坐标均大于![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程选讲
在直角坐标系![]() 中,曲线C1的参数方程为
中,曲线C1的参数方程为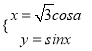 (a为参数),以原点O为极点,
(a为参数),以原点O为极点,
以x轴正半轴为极轴,建立极坐标系,曲 线C2的极坐标方程为![]()
(1)求曲线C1的普通方程与曲线C2的直角坐标方程.
(2)设P为曲线C1上的动点,求点P到C2上点的距离的最小值,并求此时点P坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
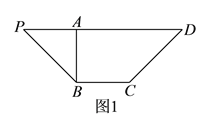
【题目】如图![]() ,等腰梯形
,等腰梯形![]() 中,
中, ![]() ,
, ![]() 于点
于点![]() ,
, ![]() ,且
,且![]() .沿
.沿![]() 把
把![]() 折起到
折起到![]() 的位置(如图
的位置(如图![]() ),使
),使![]() .
.
(I)求证: ![]() 平面
平面![]() .
.
(II)求三棱锥![]() 的体积.
的体积.
(III)线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() 平面
平面![]() ,若存在,指出点
,若存在,指出点![]() 的位置并证明;若不存在,请说明理由.
的位置并证明;若不存在,请说明理由.
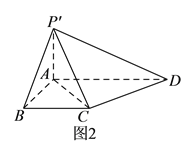
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着我国经济的快速发展,民用汽车的保有量也迅速增长.机动车保有量的发展影响到环境质量、交通安全、道路建设等诸多方面.在我国,尤其是大中型城市,机动车已成为城市空气污染的重要来源.因此,合理预测机动车保有量是未来进行机动车污染防治规划、道路发展规划等的重要前提.从2012年到2016年,根据“云南省某市国民经济和社会发展统计公报”中公布的数据,该市机动车保有量数据如表所示.
年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
机动车保有量 | 169 | 181 | 196 | 215 | 230 |
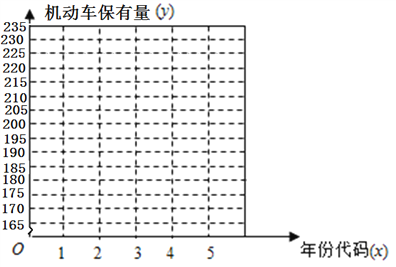
(1)在图所给的坐标系中作出数据对应的散点图;
(2)建立机动车保有量![]() 关于年份代码
关于年份代码![]() 的回归方程;
的回归方程;
(3)按照当前的变化趋势,预测2017年该市机动车保有量.
附注:回归直线方程![]() 中的斜率和截距的最小二乘估计公式分别为:
中的斜率和截距的最小二乘估计公式分别为:
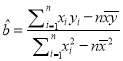 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com