
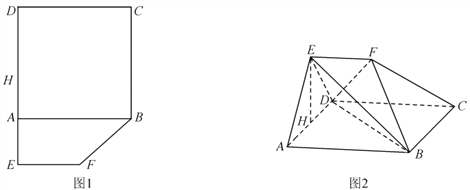
【题目】如图1,在平面多边形![]() 中,四边形
中,四边形![]() 为正方形,
为正方形, ![]() ,
, ![]() ,沿着
,沿着![]() 将图形折成图2,其中
将图形折成图2,其中![]() ,
, ![]() ,
, ![]() 为
为![]() 的中点.
的中点.
(1)求证: ![]() ;
;
(2)求四棱锥![]() 的体积.
的体积.
【答案】(1)见解析;(2)1.
【解析】试题分析:(1) 由题可知, ![]() ,
, ![]() ,且
,且![]() ,由线面垂直的判定定理可得
,由线面垂直的判定定理可得![]() 平面
平面![]() ,进而得到
,进而得到![]() ,又
,又![]() ,可证出
,可证出![]() 平面
平面![]() ,则
,则![]() ;(2)将四棱锥分割,
;(2)将四棱锥分割, ![]() , 因为
, 因为![]() ,且
,且![]() ,所以
,所以![]() ,所以
,所以![]() ,计算三棱锥E-ABD的体积即可.
,计算三棱锥E-ABD的体积即可.
试题解析:
(1)证明:由题可知, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .
.
因为![]() ,
, ![]() 是
是![]() 的中点,所以
的中点,所以![]() .
.
又![]() ,
, ![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又因为![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解: ![]() ,其中
,其中![]() .
.
因为![]() ,且
,且![]() ,所以
,所以![]() ,
,
所以![]() .
.
点睛: 求锥体的体积要充分利用多面体的截面和旋转体的轴截面,将空间问题转化为平面问题求解,注意求体积的一些特殊方法——分割法、补形法、等体积法. ①割补法:求一些不规则几何体的体积时,常用割补法转化成已知体积公式的几何体进行解决.②等积法:等积法包括等面积法和等体积法.等积法的前提是几何图形(或几何体)的面积(或体积)通过已知条件可以得到,利用等积法可以用来求解几何图形的高或几何体的高,特别是在求三角形的高和三棱锥的高时,这一方法回避了通过具体作图得到三角形(或三棱锥)的高,而通过直接计算得到高的数值.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】设A1、A2为椭圆 ![]() 的左右顶点,若在椭圆上存在异于A1、A2的点P,使得
的左右顶点,若在椭圆上存在异于A1、A2的点P,使得 ![]() ,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
,其中O为坐标原点,则椭圆的离心率e的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , a1=1,且(n+1)an=2Sn(n∈N*),数列{bn}满足 ![]() ,
, ![]() ,对任意n∈N* , 都有
,对任意n∈N* , 都有 ![]() .
.
(1)求数列{an}、{bn}的通项公式;
(2)令Tn=a1b1+a2b2+…+anbn . 若对任意的n∈N* , 不等式λnTn+2bnSn<2(λn+3bn)恒成立,试求实数λ的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某小区随机抽取40个家庭,收集了这40个家庭去年的月均用水量(单位:吨)的数据,整理得到频数分布表和频率分布直方图.
分组 | 频数 |
[2,4) | 2 |
[4,6) | 10 |
[6,8) | 16 |
[8,10) | 8 |
[10,12] | 4 |
合计 | 40 |
(1)求频率分布直方图中a,b的值;
(2)从该小区随机选取一个家庭,试估计这个家庭去年的月均用水量不低于6吨的概率;
(3)在这40个家庭中,用分层抽样的方法从月均用水量不低于6吨的家庭里抽取一个容量为7的样本,将该样本看成一个总体,从中任意选取2个家庭,求其中恰有一个家庭的月均用水量不低于8吨的概率. 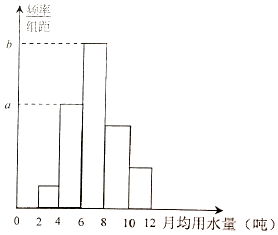
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的一边AB在x轴上,另一边CD在x轴上方,且AB=8,BC=6,其中A(﹣4,0)、B(4,0). 
(1)若A、B为椭圆的焦点,且椭圆经过C、D两点,求该椭圆的方程;
(2)若A、B为双曲线的焦点,且双曲线经过C、D两点,求双曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①函数 ![]() 是奇函数;
是奇函数;
②存在实数α,使得sinα+cosα= ![]() ;
;
③若α,β是第一象限角且α<β,则tanα<tanβ;
④ ![]() 是函数
是函数 ![]() 的一条对称轴方程;
的一条对称轴方程;
⑤函数 ![]() 的图象关于点
的图象关于点 ![]() 成中心对称图形.
成中心对称图形.
其中命题正确的是(填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了得到函数y=2sin( ![]() ),x∈R的图象只需把函数y=2sinx,x∈R的图象上所有的点( )
),x∈R的图象只需把函数y=2sinx,x∈R的图象上所有的点( )
A.向右平移 ![]() 个单位长度,再把所有各点的横坐标缩短到原来的
个单位长度,再把所有各点的横坐标缩短到原来的 ![]() 倍
倍
B.向左平移 ![]() 个单位长度,再把所有各点的横坐标伸长到原来的3倍
个单位长度,再把所有各点的横坐标伸长到原来的3倍
C.向左平移 ![]() 个单位长度,再把所有各点的横坐标缩短到原来的
个单位长度,再把所有各点的横坐标缩短到原来的 ![]() 倍
倍
D.向右平移 ![]() 个单位长度,再把所有各点的横坐标伸长到原来的3倍
个单位长度,再把所有各点的横坐标伸长到原来的3倍
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com