
等比数列 的各项均为正数,且
的各项均为正数,且 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设  ,求数列
,求数列 的前
的前 项和
项和 .
.
(1)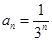 .(2)数列
.(2)数列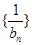 的前n项和为
的前n项和为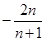
解析试题分析:(1)根据等比数列的首项和公比求通项公式;一般转化为首项和公比列方程求解,注意题中限制条件;(2)观测数列的特点形式,看使用什么方法求和.使用裂项法求和时,要注意正负项相消时消去了哪些项,保留了哪些项,切不可漏写未被消去的项,未被消去的项有前后对称的特点,实质上造成正负相消是此法的根源和目的.(3)在做题时注意观察式子特点选择有关公式和性质进行化简,这样给做题带来方便,掌握常见求和方法,如分组转化求和,裂项法,错位相减.
试题解析:解:(Ⅰ)设数列 的公比为
的公比为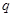 ,由
,由 得
得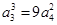 所以
所以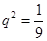 。
。
由条件可知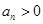 ,故
,故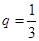 。
。
由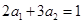 得
得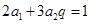 ,所以
,所以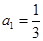 。
。
故数列 的通项式为
的通项式为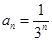 . 5分
. 5分
(Ⅱ )
故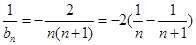 8分
8分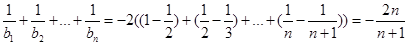
所以数列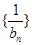 的前n项和为
的前n项和为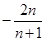 12分
12分
考点:(1)等比数列的通项公式;(2)裂项法求和.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com