Question

【题目】下列结论不正确的是（填序号）.
①各个面都是三角形的几何体是三棱锥；
②以三角形的一条边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫圆锥；
③棱锥的侧棱长与底面多边形的边长相等，则此棱锥可能是六棱锥；
④圆锥的顶点与底面圆周上的任意一点的连线都是母线.

Answer 1

【答案】①②③
【解析】①错误，如图所示，由两个结构相同的三棱锥叠放在一起构成的几何体，各面都是三角形，但它不是棱锥.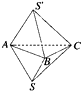

②错误，如图，若△ABC不是直角三角形或是直角三角形，但旋转轴不是直角边所在直线，所得的几何体不是圆锥.

③错误，若六棱锥的所有棱长都相等，则底面多边形是正六边形，由几何图形知，若以正六边形为底面，侧棱长必然要大于底面边长.
④正确，符合圆锥曲线母线的定义，故错误的是①②③.
所以答案是:①②③.
【考点精析】关于本题考查的棱锥的结构特征和旋转体（圆柱、圆锥、圆台），需要了解侧面、对角面都是三角形；平行于底面的截面与底面相似，其相似比等于顶点到截面距离与高的比的平方；常见的旋转体有：圆柱、圆锥、圆台、球才能得出正确答案．