
【题目】已知f(x)=2+log3x,x∈[1,9],则函数y=[f(x)]2+f(x2)的最大值为( )
A.6
B.22
C.﹣3
D.13
【答案】D
【解析】解:y=[f(x)]2+f(x2)=(log3x)2+6log3x+6,
∵f(x)=2+log3x,x∈[1,9],
∴ ![]() ,解得:1≤x≤3,
,解得:1≤x≤3,
∴y=[f(x)]2+f(x2)=(log3x)2+6log3x+6定义域是{x|1≤x≤3}.
令log3x=t,1≤x≤3,
∴0≤t≤1,
∴y=t2+6t+6,0≤t≤1,
y=t2+6t+6,在[0,1]上是增函数,
当t=1时,即x=3时,
y取最大值,最大值为13,
故选:D.
根据f(x)的定义域为[1,9],求出y=[f(x)]2+f(x2)的定义域为[1,3],然后利用二次函数的最值再求函数y=[f(x)]2+f(x2))=(log3x)2+6log3x+6,令log3x=t,1≤x≤3,0≤t≤1,由二次函数的性质即可求得函数y=[f(x)]2+f(x2).


科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() , 其中左焦点F(﹣2,0).
, 其中左焦点F(﹣2,0).
(1)求椭圆C的方程;
(2)若直线y=x+m与椭圆C交于不同的两点A,B,且线段的中点M在圆x2+y2=1上,求m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:点P在直径AB=1的半圆上移动(点P不与A,B重合),过P作圆的切线PT且PT=1,∠PAB=α,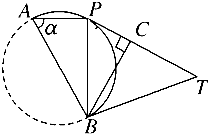
(1)当α为何值时,四边形ABTP面积最大?
(2)求|PA|+|PB|+|PC|的取值范围?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线y2=4x,过点P(2,0)作斜率分别为k1 , k2的两条直线,与抛物线相交于点A、B和C、D,且M、N分别是AB、CD的中点 
(1)若k1+k2=0, ![]() ,求线段MN的长;
,求线段MN的长;
(2)若k1k2=﹣1,求△PMN面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线的顶点与焦点分别是椭圆 ![]() =1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
=1(a>b>0)的焦点与顶点,若双曲线的两条渐近线与椭圆的交点构成的四边形恰为正方形,则椭圆的离心率为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com