
点P在曲线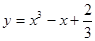 上移动,设在点P处的切线的倾斜角为为
上移动,设在点P处的切线的倾斜角为为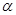 ,则
,则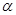 的取值范围是
的取值范围是

【解析】
试题分析:根据导数的几何意义可知切线的斜率即为该点处的导数,再根据导数的取值范围求出斜率的范围,最后再根据斜率与倾斜角之间的关系k=tanα,求出α的范围即可。解:∵tanα=3x2-1,∴tanα∈[-1,+∞).=当tanα∈[0,+∞)时,α∈[0,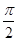 );当tanα∈[-1,0)时,α∈[,
);当tanα∈[-1,0)时,α∈[,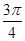 ,π).∴α∈[0,
,π).∴α∈[0,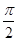 )∪[
)∪[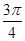 ,π).故答案
,π).故答案 。
。
考点:导数研究曲线上某点切线的方程
点评:此题考查了利用导数研究曲线上某点切线的方程,直线倾斜角与斜率的关系,以及正切函数的图象与性质.要求学生掌握导函数在某点的函数值即为过这点切线方程的斜率,且直线的斜率为倾斜角的正切值,掌握正切函数的图象与性质.


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
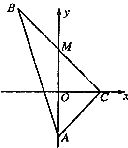
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 等恒成立,求
等恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
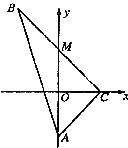 如图所示,△ABC为直角三角形,∠C=90°,若
如图所示,△ABC为直角三角形,∠C=90°,若![]() =(0,-4),M在
=(0,-4),M在![]() 轴上,且AM=
轴上,且AM=![]() ,点C在
,点C在![]() 轴上移动.
轴上移动.
(Ⅰ)求点B的轨迹E的方程;
(Ⅱ)过点F(0,![]() )的直线
)的直线![]() 与曲线E交于P、Q两点,设N(0,
与曲线E交于P、Q两点,设N(0,![]() )(
)(![]() <0),
<0),![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ≤
≤![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(Ⅲ)设以点N为圆心,以![]() 半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求
半径的圆与曲线E在第一象限的交点为H,若圆在点H处的切线与曲线E在点H处的切线互相垂直,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com