
【题目】在国家批复成立江北新区后,南京市政府规划在新区内的一条形地块上新建一个全民健身中心,规划区域为四边形ABCD,如图![]() ,
,![]() ,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知
,点B在线段OA上,点C、D分别在射线OP与AQ上,且A和C关于BD对称.已知![]() .
.
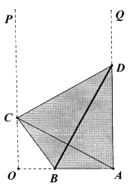
(1)若![]() ,求BD的长;
,求BD的长;
(2)问点C在何处时,规划区域的面积最小?最小值是多少?
科目:高中数学 来源: 题型:
【题目】菱形![]() 中,
中,![]()
![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,
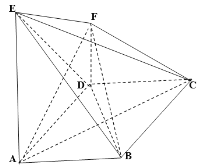
(1)证明:直线![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值;
的正弦值;
(3)线段![]() 上是否存在点
上是否存在点![]() 使得直线
使得直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() ?若存在,求
?若存在,求![]() ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 中,
中,![]() 与
与![]() 均为等腰直角三角形,且
均为等腰直角三角形,且![]() ,
,![]() ,
,![]() 为
为![]() 上一点,且
上一点,且![]() 平面
平面![]() .
.
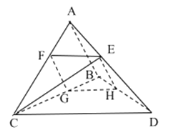
(1)求证:![]() ;
;
(2)过![]() 作一平面分别交
作一平面分别交![]() ,
, ![]() ,
, ![]() 于
于![]() ,
,![]() ,
,![]() ,若四边形
,若四边形![]() 为平行四边形,求多面体
为平行四边形,求多面体![]() 的表面积.
的表面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,A、B两地相距100公里,两地政府为提升城市的抗疫能力,决定在A、B之间选址P点建造储备仓库,共享民生物资,当点P在线段AB的中点C时,建造费用为2000万元,若点P在线段AC上(不含点A),则建造费用与P、A之间的距离成反比,若点P在线段CB上(不含点B),则建造费用与P、B之间的距离成反比,现假设P、A之间的距离为x千米![]() ,A地所需该物资每年的运输费用为
,A地所需该物资每年的运输费用为![]() 万元,B地所需该物资每年的运输费用为
万元,B地所需该物资每年的运输费用为![]() 万元,
万元,![]() 表示建造仓库费用,
表示建造仓库费用,![]() 表示两地物资每年的运输总费用(单位:万元).
表示两地物资每年的运输总费用(单位:万元).
![]()
(1)求函数![]() 的解析式;
的解析式;
(2)若规划仓库使用的年限为![]() ,
,![]() ,求
,求![]() 的最小值,并解释其实际意义.
的最小值,并解释其实际意义.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() :
:![]() 的离心率
的离心率![]() ,其左焦点
,其左焦点![]() 到此双曲线渐近线的距离为
到此双曲线渐近线的距离为![]() .
.
(1)求双曲线![]() 的方程;
的方程;
(2)若过点![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点,且以
两点,且以![]() 为直径的圆
为直径的圆![]() 过原点
过原点![]() ,求圆
,求圆![]() 的圆心到抛物线
的圆心到抛物线![]() 的准线的距离.
的准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂为提高生产效率,需引进一条新的生产线投入生产,现有两条生产线可供选择,生产线①:有A,B两道独立运行的生产工序,且两道工序出现故障的概率依次是0.02,0.03.若两道工序都没有出现故障,则生产成本为15万元;若A工序出现故障,则生产成本增加2万元;若B工序出现故障,则生产成本增加3万元;若A,B两道工序都出现故障,则生产成本增加5万元.生产线②:有a,b两道独立运行的生产工序,且两道工序出现故障的概率依次是0.04,0.01.若两道工序都没有出现故障,则生产成本为14万元;若a工序出现故障,则生产成本增加8万元;若b工序出现故障,则生产成本增加5万元;若a,b两道工序都出现故障,则生产成本增加13万元.
(1)若选择生产线①,求生产成本恰好为18万元的概率;
(2)为最大限度节约生产成本,你会给工厂建议选择哪条生产线?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外卖平台为提高外卖配送效率,针对外卖配送业务提出了两种新的配送方案,为比较两种配送方案的效率,共选取50名外卖骑手,并将他们随机分成两组,每组25人,第一组骑手用甲配送方案,第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量(单位:单)绘制了如下茎叶图:
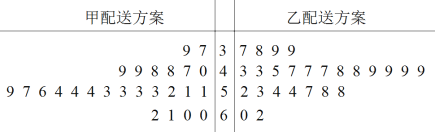
(1)根据茎叶图,求各组内25位骑手完成订单数的中位数,已知用甲配送方案的25位骑手完成订单数的平均数为52,结合中位数与平均数判断哪种配送方案的效率更高,并说明理由;
(2)设所有50名骑手在相同时间内完成订单数的平均数![]() ,将完成订单数超过
,将完成订单数超过![]() 记为“优秀”,不超过
记为“优秀”,不超过![]() 记为“一般”,然后将骑手的对应人数填入下面列联表;
记为“一般”,然后将骑手的对应人数填入下面列联表;
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根据(2)中的列联表,判断能否有![]() 的把握认为两种配送方案的效率有差异.
的把握认为两种配送方案的效率有差异.
附: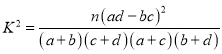 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com