
【题目】已知椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]()
(1)求椭圆![]() 的标准方程
的标准方程
(2)是否存在过点![]() 的直线
的直线![]() 交椭圆与不同的两点
交椭圆与不同的两点![]() ,且满足
,且满足![]() (其中
(其中![]() 为坐标原点)。若存在,求出直线
为坐标原点)。若存在,求出直线![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
【答案】(1)![]() ;(2)存在直线
;(2)存在直线![]() 或
或![]() 满足题意.
满足题意.
【解析】
(1)根据已知得到关于a,b,c的方程组,解方程组即得解.(2)对直线l的斜率分类讨论,直线![]() 的斜率必存在,不妨设为
的斜率必存在,不妨设为![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,即
,即![]() ,联立直线和椭圆的方程得到
,联立直线和椭圆的方程得到![]() ,得到
,得到![]() ,把韦达定理代入向量的数量积,得到k的值.即得直线的方程.
,把韦达定理代入向量的数量积,得到k的值.即得直线的方程.
(1)∵椭圆![]() 过点
过点![]() ,且离心率
,且离心率![]()
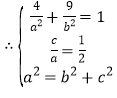 ,解得
,解得![]() ,
,
∴椭圆的方程为![]()
(2)假设存在过点![]() 的直线
的直线![]() 交椭圆于不同的两点
交椭圆于不同的两点![]() ,且满足
,且满足![]()
若直线![]() 的斜率不存在,且直线过点
的斜率不存在,且直线过点![]() ,则直线
,则直线![]() 即为
即为![]() 轴所在直线
轴所在直线
∴直线![]() 与椭圆的两不同交点
与椭圆的两不同交点![]() 就是椭圆短轴的端点,
就是椭圆短轴的端点,
![]()
![]()
∴直线![]() 的斜率必存在,不妨设为
的斜率必存在,不妨设为![]() ,
,
∴可设直线![]() 的方程为
的方程为![]() ,即
,即![]()
联立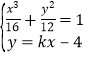 ,消
,消![]() 得
得![]() ,
,
∵直线与椭圆相交于不同的两点![]() ,
,
![]() 得:
得: ![]() 或
或![]() ①
①
设![]() ,
,
![]()
![]()
又![]() ,
,
![]()
化简得![]() ,
,
![]() 或
或![]() ,经检验均满足①式,
,经检验均满足①式,
∴直线![]() 的方程为:
的方程为: ![]() 或
或![]() ,
,
∴存在直线![]() 或
或![]() 满足题意.
满足题意.


科目:高中数学 来源: 题型:
【题目】在下列命题中,下列选项正确的是( )
A. 在回归直线![]() 中,变量
中,变量![]() 时,变量
时,变量![]() 的值一定是15.
的值一定是15.
B. 两个变量相关性越强,则相关系数![]() 就越接近于1.
就越接近于1.
C. 在残差图中,残差点比较均匀落在水平的带状区域中即可说明选用的模型比较合适,与带状区域的宽度无关.
D. 若![]() 是两个相等的非零实数,则
是两个相等的非零实数,则![]() 是纯虚数.
是纯虚数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣bx+alnx.
(1)若b=2,函数f(x)有两个极值点x1 , x2 , 且x1<x2 , 求实数a的取值范围;
(2)在(1)的条件下,证明:f(x2)>﹣ ![]() ;
;
(3)若对任意b∈[1,2],都存在x∈(1,e)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点M(﹣3,0),点P在y轴上,点Q在x轴的正半轴上,点N在直线PQ上,且满足 ![]() . (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
. (Ⅰ)当点P在y轴上移动时,求点N的轨迹C的方程;
(Ⅱ)过点 ![]() 做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
做直线l与轨迹C交于A,B两点,若在x轴上存在一点E(x0 , 0),使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某算法的程序框图如图所示,其中输入的变量x在1,2,3,…,24这24个整数中等可能随机产生 (I)分别求出按程序框图正确编程运行时输出y的值为i的概率pi(i=1,2,3);
(II)甲乙两同学依据自己对程序框图的理解,各自编程写出程序重复运行n次后,统计记录输出y的值为i(i=1,2,3)的频数,以下是甲乙所作频数统计表的部分数据.
甲的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 14 | 6 | 10 |
… | … | … | … |
2100 | 1027 | 376 | 697 |
乙的频数统计图(部分)
运行次数n | 输出y的值为1的频数 | 输出y的值为2的频数 | 输出y的值为3的频数 |
30 | 12 | 11 | 7 |
… | … | … | … |
2100 | 1051 | 696 | 353 |
当n=2100时,根据表中的数据,分别写出甲、乙所编程序各自输出y的值为i(i=1,2,3)的频率(用分数表示),并判断两位同学中哪一位所编程序符合要求的可能系较大;
(III)将按程序摆图正确编写的程序运行3次,求输出y的值为2的次数ξ的分布列及数学期望.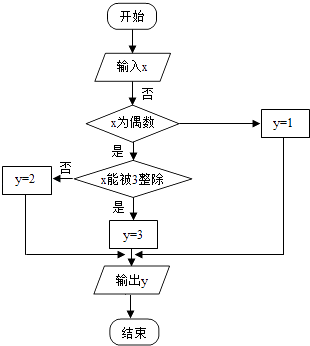
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给定命题p:“若a2017>﹣1,则a>﹣1”;命题q:“x∈R,x2tanx2>0”,则下列命题中,真命题的是( )
A.p∨q
B.(¬p)∨q
C.(¬p)∧q
D.(¬p)∧(¬q)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com