
【题目】如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.求证: (Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC⊥平面BDE.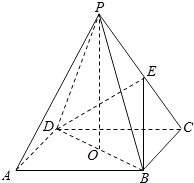
【答案】证明:(I)∵O是AC的中点,E是PC的中点, ∴OE∥AP,又∵OE平面BDE,PA
平面BDE.
∴PA∥平面BDE.
(II)∵PO⊥底面ABCD,PO⊥BD,
又∵AC⊥BD,且AC∩PO=O
∴BD⊥平面PAC,而BD平面BDE,
∴平面PAC⊥平面BDE
【解析】(I)根据线面平行的判定定理证出即可;(II)根据面面垂直的判定定理证明即可.
【考点精析】解答此题的关键在于理解直线与平面平行的判定的相关知识,掌握平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行;简记为:线线平行,则线面平行,以及对平面与平面垂直的判定的理解,了解一个平面过另一个平面的垂线,则这两个平面垂直.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知曲线C1的参数方程为 ![]() (φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4
(φ为参数).以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=4 ![]() cosθ.
cosθ.
(1)求C1与C2交点的直角坐标;
(2)已知曲线C3的参数方程为 ![]() (0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
(0≤α<π,t为参数,且t≠0),C3与C1相交于点P,C2与C3相交于点Q,且|PQ|=8,求α的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某产品的历史收益率的频率分布直方图如图所示.
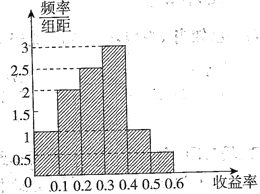
(1)试估计该产品收益率的中位数;
(2)若该产品的售价![]() (元)与销量
(元)与销量![]() (万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组
(万份)之间有较强线性相关关系,从历史销售记录中抽样得到如表5组![]() 与
与![]() 的对应数据:
的对应数据:
售价 | 25 | 30 | 38 | 45 | 52 |
销量 | 7.5 | 7.1 | 6.0 | 5.6 | 4.8 |
根据表中数据算出![]() 关于
关于![]() 的线性回归方程为
的线性回归方程为![]() ,求
,求![]() 的值;
的值;
(3)若从表中五组销量数据中随机抽取两组,记其中销量超过6万份的组数为![]() ,求
,求![]() 的分布列及期望.
的分布列及期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知,圆C:x2+y2﹣8y+12=0,直线l:ax+y+2a=0.
(1)当a为何值时,直线l与圆C相切;
(2)当直线l与圆C相交于A、B两点,且AB=2 ![]() 时,求直线l的方程.
时,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,f(x)在[0,+∞)上是增函数,且f( ![]() )=0,则不等式f(
)=0,则不等式f( ![]() )>0的解集为( )
)>0的解集为( )
A.(0, ![]() )∪(2,+∞)
)∪(2,+∞)
B.( ![]() ,1)∪(2,+∞)??
,1)∪(2,+∞)??
C.(0, ![]() )
)
D.(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“1+2+22+…+2n-1=2n-1(n∈N+)”的过程中,第二步n=k时等式成立,则当n=k+1时,应得到( )
A.1+2+22+…+2k-2+2k-1=2k+1-1
B.1+2+22+…+2k+2k+1=2k-1+2k+1
C.1+2+22+…+2k-1+2k+1=2k+1-1
D.1+2+22+…+2k-1+2k=2k+1-1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用数学归纳法证明“当 n 为正奇数时,xn+yn 能被 x+y 整除”,第二步归纳假
设应该写成( )
A.假设当n=k![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
B.假设当N=2K ![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
C.假设当N=2K+1 ![]() 时, xk+yk 能被 x+y 整除
时, xk+yk 能被 x+y 整除
D.假设当 N=2K-1![]() 时, x2k-1+y2k-1 能被 x+y 整除
时, x2k-1+y2k-1 能被 x+y 整除
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com