
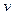 海里/时(4≤
海里/时(4≤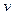 ≤20)从
≤20)从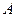 港出发到距50海里的
港出发到距50海里的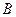 港去,然后乘汽车以
港去,然后乘汽车以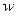 千米/时(30≤
千米/时(30≤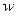 ≤100)自
≤100)自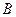 港向距300千米的
港向距300千米的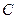 市驶去,应该在同一天下午4至9点到达
市驶去,应该在同一天下午4至9点到达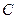 市.设汽车、摩托艇所需的时间分别是
市.设汽车、摩托艇所需的时间分别是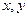 小时.
小时.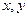 所满足的条件,并在所给的平面直角坐标系内,作出表示
所满足的条件,并在所给的平面直角坐标系内,作出表示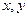 范围的图形;
范围的图形;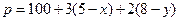 (元),那么
(元),那么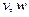 分别是多少时走得最经济?此时需花费多少元?
分别是多少时走得最经济?此时需花费多少元?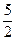 ≤y≤
≤y≤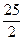 ⑵x=10,v=12.5,w=30,p的最小值为93元
⑵x=10,v=12.5,w=30,p的最小值为93元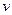 =
=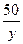 ,
,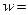
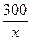 ,4≤
,4≤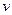 ≤20,30≤
≤20,30≤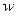 ≤100,
≤100, 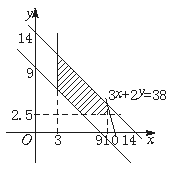
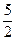 ≤y≤
≤y≤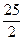 .①
.①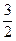 的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当y=4时,p最小,此时x=10,v=12.5,w=30,p的最小值为93元.
的直线3x+2y=k中,使k值最大的直线必通过点(10,4),即当y=4时,p最小,此时x=10,v=12.5,w=30,p的最小值为93元.

科目:高中数学 来源:不详 题型:解答题
| 鱼类 | 鱼料A | 鱼料B | 鱼料C |
| 鲫鱼/kg | 15g | 5g | 8g |
| 鲤鱼/kg | 8g | 5g | 18g |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 产品 产品消耗量 资源 | 甲产品 (每吨) | 乙产品 (每吨) | 资源限额 (每天) |
| 煤(t) | 9 | 4 | 360 |
| 电力(kw·h) | 4 | 5 | 200 |
| 劳力(个) | 3 | 10 | 300 |
| 利润(万元) | 6 | 12 | |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com