
【题目】设直线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() 相交于
相交于![]() ,
,![]() 两个不同的点,与
两个不同的点,与![]() 轴相交于点
轴相交于点![]() ,记
,记![]() 为坐标原点.
为坐标原点.
(1)证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题分析:(1)设直线![]() 的方程为
的方程为![]() ,将直线的方程代入抛物线的方程,消去
,将直线的方程代入抛物线的方程,消去![]() 得到关于
得到关于![]() 的一元二次方程,再结合直线
的一元二次方程,再结合直线![]() 与椭圆相交于两个不同的点得到根的判别式大于
与椭圆相交于两个不同的点得到根的判别式大于![]() ,从而解决问题;(2)设
,从而解决问题;(2)设![]() ,
,![]() ,由(1)得
,由(1)得![]() ,由
,由![]() ,得
,得![]() 从而求得
从而求得![]() 的面积,最后利用基本不等式求得其最大值,及取得最大值时的
的面积,最后利用基本不等式求得其最大值,及取得最大值时的![]() 值,从而即可求得
值,从而即可求得![]() 的面积取得最大值时的椭圆方程.
的面积取得最大值时的椭圆方程.
试题解析:(1)依题意,直线![]() 显然不平行于坐标轴,故
显然不平行于坐标轴,故![]() 可化为
可化为![]() ,
,
将![]() 代入
代入![]() ,整理得
,整理得![]() ,①
,①
由直线![]() 与椭圆相交于两个不同的点,得
与椭圆相交于两个不同的点,得![]() ,
,
化简整理即得![]() .(*)
.(*)
(2)![]() ,
,![]() ,由①,得
,由①,得![]() ,②
,②
因为![]() ,
,![]() ,由
,由![]() ,得
,得![]() ,③
,③
由②③联立,解得![]() ,④
,④
![]() 的面积
的面积![]()
![]() ,
,
上式取等号的条件是![]() ,即
,即![]() .
.
当![]() 时,由④解得
时,由④解得![]() ;当
;当![]() 时,由④解得
时,由④解得![]() .
.
将![]() ,
,![]() 及
及![]() ,
,![]() 这两组值分别代入①,
这两组值分别代入①,
均可解出![]() ,
,
经验证,![]() ,
,![]() 满足(*)式.
满足(*)式.
所以,![]() 的面积取得最大值时椭圆方程为
的面积取得最大值时椭圆方程为![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】定义在R上的偶函数f(x),对任意x1 , x2∈[0,+∞)(x1≠x2),有 ![]() <0,则( )
<0,则( )
A.f(3)<f(﹣2)<f(1)
B.f(1)<f(﹣2)<f(3)
C.f(﹣2)<f(1)<f(3)
D.f(3)<f(1)<f(﹣2)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)=2x2﹣4x.
(1)指出图象的开口方向、对称轴方程、顶点坐标;
(2)用描点法画出它的图象;
(3)求出函数的最值,并分析函数的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校从参加高二年级期末考试的学生中抽出60名学生,并统计了他们的化学成绩(成绩均为整数且满分为100分),把其中不低于50分的分成五段![]() ,
,![]() ,…,
,…,![]() 后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如图部分频率分布直方图.观察图形的信息,回答下列问题:
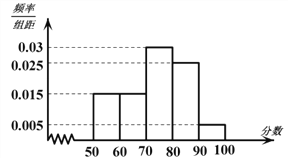
(1)求出这60名学生中化学成绩低于50分的人数;
(2)估计高二年级这次考试化学学科及格率(60分以上为及格);
(3)从化学成绩不及格的学生中随机调查1人,求他的成绩低于50分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() :
: ![]() 和点
和点![]() ,动圆
,动圆![]() 经过点
经过点![]() 且与圆
且与圆![]() 相切,圆心
相切,圆心![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)点![]() 是曲线
是曲线![]() 与
与![]() 轴正半轴的交点,点
轴正半轴的交点,点![]() ,
, ![]() 在曲线
在曲线![]() 上,若直线
上,若直线![]() ,
, ![]() 的斜率分别是
的斜率分别是![]() ,
, ![]() ,满足
,满足![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知下图中,四边形 ABCD是等腰梯形, ![]() ,
, ![]() ,
, ![]() 于M、交EF于点N,
于M、交EF于点N, ![]() ,
, ![]() ,现将梯形ABCD沿EF折起,记折起后C、D为
,现将梯形ABCD沿EF折起,记折起后C、D为![]() 、
、![]() 且使
且使![]() ,如图示.
,如图示.
![]()
![]()

(Ⅰ)证明: ![]()
![]() 平面ABFE;,
平面ABFE;,
(Ⅱ)若图6中, ![]() ,求点M到平面
,求点M到平面![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com