
【题目】试分别用综合法、分析法、反证法等三种方法,证明下列结论:已知0<a<1,则 ![]() +
+ ![]() ≥9.
≥9.
【答案】证明:分析法: ![]() +
+ ![]() ≥9
≥9 ![]() ≥9
≥9 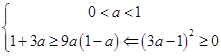
反证法:假设 ![]() +
+ ![]() <9,通分得
<9,通分得 ![]() <9.
<9.
∵0<a<1,∴1+3a<9a(1﹣a),整理得(3a﹣1)2<0,这与平方数不小于0矛盾.
∴假设不成立,则 ![]() +
+ ![]() ≥9.
≥9.
综合法:由(3a﹣1)2≥0,变形得1+3a≥9a(1﹣a).
∵0<a<1,∴ ![]() ≥9,即
≥9,即 ![]() +
+ ![]() ≥9.
≥9.
【解析】分析法是从结论出发找出要证结论的充分条件;反证法是假设结论不成立,从假设出发:同分;两边同时乘以a(1﹣a);得到不成立的结论,从而得证;综合法即将分析法的每一步倒过来.
【考点精析】解答此题的关键在于理解反证法的相关知识,掌握从命题结论的反面出发(假设),引出(与已知、公理、定理…)矛盾,从而否定假设证明原命题成立,这样的证明方法叫做反证法.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:
【题目】如图,已知二面角α﹣MN﹣β的大小为60°,菱形ABCD在面β内,A、B两点在棱MN上,∠BAD=60°,E是AB的中点,DO⊥面α,垂足为O. 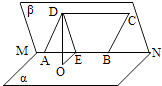
(1)证明:AB⊥平面ODE;
(2)求异面直线BC与OD所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点![]() 的椭圆
的椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,
, ![]() 为椭圆上的任意一点,且
为椭圆上的任意一点,且![]() 成等差数列.
成等差数列.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)直线![]() 交椭圆于
交椭圆于![]() 两点,若点
两点,若点![]() 始终在以
始终在以![]() 为直径的圆外,求实数
为直径的圆外,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】海中一小岛![]() 的周围
的周围![]()
![]() 内有暗礁,海轮由西向东航行至
内有暗礁,海轮由西向东航行至![]() 处测得小岛
处测得小岛![]() 位于北偏东
位于北偏东![]() ,航行8
,航行8![]() 后,于
后,于![]() 处测得小岛
处测得小岛![]() 在北偏东
在北偏东![]() (如图所示).
(如图所示).

(1)如果这艘海轮不改变航向,有没有触礁的危险?请说明理由.
(2)如果有触礁的危险,这艘海轮在![]() 处改变航向为东偏南
处改变航向为东偏南![]() (
(![]() )方向航行,求
)方向航行,求![]() 的最小值.
的最小值.
附: ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义运算: ![]() ;,例如23=3,则下列等式不能成立的是( )
;,例如23=3,则下列等式不能成立的是( )
A.ab=ba
B.(ab)c=a(bc)
C.(ab)2=a2b2
D.c(ab)=(ca)(cb)(c>0)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆C过点A(6,4),B(1,﹣1),且圆心在直线l:x﹣5y+7=0上.
(1)求圆C的方程;
(2)P为圆C上的任意一点,定点Q(7,0),求线段PQ中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球. (I)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com