
【题目】![]() 是偶函数,且在(0,+∞)是减函数,则整数a的值是 .
是偶函数,且在(0,+∞)是减函数,则整数a的值是 .
【答案】﹣1、1、3、5
【解析】解:∵函数 ![]() 是(0,+∞)是减函数 ∴a2﹣4a﹣9<0
是(0,+∞)是减函数 ∴a2﹣4a﹣9<0
∴ ![]()
∵a为整数
∴a=﹣1、0、1、2、3、4、5
∴当a=﹣1时,y=x﹣4是偶函数;
当a=0时,y=x﹣9是奇函数;
当a=1时,y=x﹣12是偶函数;
当a=2时,y=x﹣13是奇函数;
当a=3时,y=x﹣12是偶函数
当a=4时,y=x﹣9是奇函数;
当a=5时,y=x﹣4是偶函数.
∴a=﹣1、1、3、5
所以答案是:﹣1、1、3、5.
【考点精析】掌握函数奇偶性的性质是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】某理科考生参加自主招生面试,从7道题中(4道理科题3道文科题)不放回地依次任取3道作答.
(1)求该考生在第一次抽到理科题的条件下,第二次和第三次均抽到文科题的概率;
(2)规定理科考生需作答两道理科题和一道文科题,该考生答对理科题的概率均为![]() ,答对文科题的概率均为
,答对文科题的概率均为![]() ,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分
,若每题答对得10分,否则得零分.现该生已抽到三道题(两理一文),求其所得总分![]() 的分布列与数学期望
的分布列与数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点.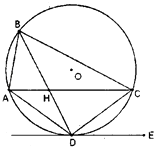
(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点相同,
的焦点相同,![]() ,
,![]() 为椭圆的左、右焦点.
为椭圆的左、右焦点.![]() 为椭圆上任意一点,△
为椭圆上任意一点,△![]() 面积的最大值为1.
面积的最大值为1.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() :
:![]()
![]() 交椭圆
交椭圆![]() 于
于![]() ,
,![]() 两点.
两点.
(i)若直线![]() 与
与![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,且
,且![]() ,求证:直线
,求证:直线![]() 过定点,并求出该定点的坐标;
过定点,并求出该定点的坐标;
(ii)若直线![]() 的斜率时直线
的斜率时直线![]() ,
,![]() 斜率的等比中项,求△
斜率的等比中项,求△![]() 面积的取值范围.
面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设a为实数,函数f(x)=2x2+(x﹣a)|x﹣a|.
(1)若f(0)≥1,求a的取值范围;
(2)求f(x)的最小值;
(3)设函数h(x)=f(x),x∈(a,+∞),求不等式h(x)≥1的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(0,2)为圆C:x2+y2﹣2ax﹣2ay=0(a>0)外一点,圆C上存在点P使得∠CAP=45°,则实数a的取值范围是( )
A.(0,1)
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com