
【题目】已知定义在[﹣1,1]的函数满足f(﹣x)=﹣f(x),当a,b∈[﹣1,0)时,总有 ![]() >0(a≠b),若f(m+1)>f(2m),则实数m的取值范围是 .
>0(a≠b),若f(m+1)>f(2m),则实数m的取值范围是 .
【答案】![]()
【解析】解:∵函数f(x)满足f(﹣x)=﹣f(x),∴函数f(x)是奇函数.
又∵当a,b∈[﹣1,0)时,总有 ![]() >0,
>0,
∴函数f(x)在[﹣1,0)上单调递增函数
根据奇函数的性质可知函数f(x)在[﹣1,1]上单调递增函数
∵f(m+1)>f(2m),
∴﹣1≤2m<m+1≤1,
∴ ![]() .
.
所以答案是 ![]() .
.
【考点精析】根据题目的已知条件,利用函数奇偶性的性质的相关知识可以得到问题的答案,需要掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:
【题目】解答题。
(1)已知集合A={x|ax2﹣3x+1=0,a∈R},若A中只有一个元素,求a的取值范围.
(2)集合A={x|x2﹣6x+5<0},C={x|3a﹣2<x<4a﹣3},若CA,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某商店一个月内每天的顾客人数进行统计,得到样本的茎叶图(如图所示).则该样本的中位数、众数、极差分别是( ) 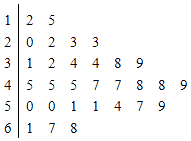
A.46 45 56
B.46 45 53
C.47 45 56
D.45 47 53
查看答案和解析>>
科目:高中数学 来源: 题型:
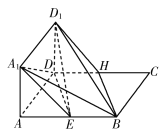
【题目】
如图所示,正方形![]() 与矩形
与矩形![]() 所在平面互相垂直,
所在平面互相垂直,![]() .
.
(1)若点![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,求证:平面
的中点,求证:平面![]() 平面
平面![]() ;
;
(2)在线段![]() 上是否存在一点
上是否存在一点![]() ,使二面角
,使二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=m﹣ ![]()
(1)若f(x)是R上的奇函数,求m的值
(2)用定义证明f(x)在R上单调递增
(3)若f(x)值域为D,且D[﹣3,1],求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P表示一个点,a,b表示两条直线,α,β表示两个平面,给出下列四个命题,其中正确的命题是( )
①P∈a,P∈αaα
②a∩b=P,bβaβ
③a∥b,aα,P∈b,P∈αbα
④α∩β=b,P∈α,P∈βP∈b.
A.①②
B.②③
C.①④
D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果函数f(x)= ![]() (m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[
(m﹣2)x2+(n﹣8)x+1(m≥0,n≥0)在区间[ ![]() ,2]上单调递减,那么mn的最大值为( )
,2]上单调递减,那么mn的最大值为( )
A.16
B.18
C.25
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】观察下列等式
l+2+3+…+n= ![]() n(n+l);
n(n+l);
l+3+6+…+ ![]() n(n+1)=
n(n+1)= ![]() n(n+1)(n+2);
n(n+1)(n+2);
1+4+10+… ![]() n(n+1)(n+2)=
n(n+1)(n+2)= ![]() n(n+1)(n+2)(n+3);
n(n+1)(n+2)(n+3);
可以推测,1+5+15+…+ ![]() n(n+1)(n+2)(n+3)= .
n(n+1)(n+2)(n+3)= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com