
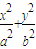 =1(a>b>0)的左右焦点分别为F1,F2,焦距为2c,若直线y=
=1(a>b>0)的左右焦点分别为F1,F2,焦距为2c,若直线y=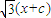 与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 .
与椭圆Γ的一个交点满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于 . 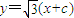 可知斜率为
可知斜率为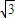 ,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,可得
,可得直线的倾斜角α=60°.又直线与椭圆Γ的一个交点M满足∠MF1F2=2∠MF2F1,可得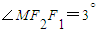 ,进而
,进而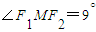 .
.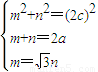 ,解出a,c即可.
,解出a,c即可.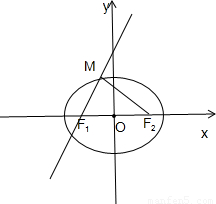 由直线
由直线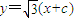 可知倾斜角α与斜率
可知倾斜角α与斜率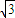 有关系
有关系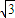 =tanα,∴α=60°.
=tanα,∴α=60°.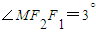 ,∴
,∴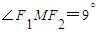 .
.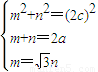 ,解得
,解得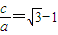 .
.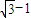 .
. .
.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:高中数学 来源: 题型:
| x2 |
| a2 |
| y2 |
| b2 |
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•潍坊二模)如图,已知F(2,0)为椭圆
(2012•潍坊二模)如图,已知F(2,0)为椭圆| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
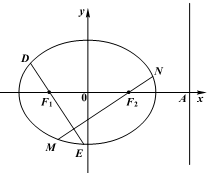 (2011•天津模拟)设椭圆
(2011•天津模拟)设椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF1 |
| AF2 |
| 27 |
| 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com