
【题目】已知椭圆C: ![]() (a>b>0 ) 经过点 P(1,
(a>b>0 ) 经过点 P(1, ![]() ),离心率 e=
),离心率 e= ![]()
(Ⅰ)求椭圆C的标准方程.
(Ⅱ)设过点E(0,﹣2 ) 的直线l 与C相交于P,Q两点,求△OPQ 面积的最大值.
【答案】解:(Ⅰ)由点 ![]() 在椭圆上得,
在椭圆上得, ![]() ①
①
又e= ![]() =
= ![]() ②,c2=a2﹣b2③
②,c2=a2﹣b2③
由①②③得c2=3,a2=4,b2=1,
故椭圆C的标准方程为 ![]() .
.
(Ⅱ)当直线l的斜率不存在,不合题意,可设直线l:y=kx﹣2,P(x1 , y1),Q(x2 , y2),
将y=kx﹣2代入椭圆方程x2+4y2=4,可得(1+4k2)x2﹣16kx+12=0,
由△=162k2﹣48(1+4k2)>0,解得k> ![]() 或k<﹣
或k<﹣ ![]() .
.
x1+x2= ![]() ,x1x2=
,x1x2= ![]() ,
,
|PQ|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]()
![]() =4
=4 ![]()
![]() ,
,
又O到直线PQ的距离d= ![]() ,
,
则S△OPQ= ![]() d|PQ|=4
d|PQ|=4 ![]() ,
,
设t= ![]() ,(t>0),则4k2=3+t2 ,
,(t>0),则4k2=3+t2 ,
即有S△OPQ= ![]() =
= ![]()
由t+ ![]() ≥2
≥2 ![]() =4,
=4,
当且仅当t=2,即k=± ![]() 时等号成立,足判别式大于0.
时等号成立,足判别式大于0.
则S△OPQ≤1.
故△OPQ 面积的最大值为1
【解析】(Ⅰ)运用椭圆的离心率公式和点满足椭圆方程,以及a,b,c的关系,解方程可得a,b,进而得到椭圆方程;(Ⅱ)当直线l的斜率不存在,不合题意,可设直线l:y=kx﹣2,P(x1 , y1),Q(x2 , y2),联立椭圆方程,消去y,得到x的方程,运用判别式大于0和韦达定理,以及弦长公式,点到直线的距离公式,由三角形的面积公式,运用换元法和基本不等式即可得到所求最大值.


 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案科目:高中数学 来源: 题型:
【题目】数列{an}满足a1= ![]() ,an+1﹣an+anan+1=0(n∈N*).
,an+1﹣an+anan+1=0(n∈N*).
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)求证:a1+a1a2+a1a2a3+…+a1a2…an<1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C经过点A(1,1)和B(4,﹣2),且圆心C在直线l:x+y+1=0上.
(Ⅰ)求圆C的标准方程;
(Ⅱ)设M,N为圆C上两点,且M,N关于直线l对称,若以MN为直径的圆经过原点O,求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】计算下列几个式子,结果为 ![]() 的序号是 ①tan25°+tan35°
的序号是 ①tan25°+tan35° ![]() tan25°tan35°,
tan25°tan35°,
② ![]() ,
,
③2(sin35°cos25°+sin55°cos65°),
④ ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f ( x)= ![]() x2 , g ( x)=a ln x(a>0).
x2 , g ( x)=a ln x(a>0).
(Ⅰ)求函数 F ( x)=f(x)g(x)的极值
(Ⅱ)若函数 G( x)=f(x)﹣g(x)+(a﹣1)在区间 ( ![]() ,e) 内有两个零点,求的取值范围;
,e) 内有两个零点,求的取值范围;
(Ⅲ)函数 h( x)=g ( x )﹣x+ ![]() ,设 x1∈(0,1),x2∈(1,+∞),若 h( x 2)﹣h( x 1)存在最大值,记为 M (a),则当 a≤e+1
,设 x1∈(0,1),x2∈(1,+∞),若 h( x 2)﹣h( x 1)存在最大值,记为 M (a),则当 a≤e+1 ![]() 时,M (a) 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
时,M (a) 是否存在最大值?若存在,求出其最大值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在长方体ABCD﹣A1B1C1D1中,E是CD上一点,AB=AD=3,AA1=2,CE=1,P是AA1上一点,且DP∥平面AEB1 , F是棱DD1与平面BEP的交点,则DF的长为( ) 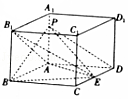
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高中生共有2700人,其中高一年级900人,高二年级1200人,高三年级600人,现采取分层抽样法抽取容量为135的样本,那么高一,高二,高三各年级抽取的人数分别为( )
A.45,75,15
B.45,45,45
C.30,90,15
D.45,60,30
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com