
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的一个焦点是F(1,0),且离心率为
=1(a>b>0)的一个焦点是F(1,0),且离心率为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设经过点F的直线交椭圆C于M,N两点,线段MN的垂直平分线交y轴于点P(0,y0),求y0的取值范围.
【答案】(1)![]() +
+![]() =1. (2)
=1. (2)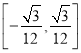
【解析】
试题解:(Ⅰ)设椭圆C的半焦距是c.依题意,得c=1.
因为椭圆C的离心率为![]() ,
,
所以a=2c=2,b2=a2-c2=3.
故椭圆C的方程为![]() +
+![]() =1.
=1.
(Ⅱ)当MN⊥x轴时,显然y0=0.
当MN与x轴不垂直时,可设直线MN的方程为
y=k(x-1)(k≠0).
由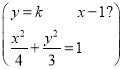
消去y并整理得(3+4k2)x2-8k2x+4(k2-3)=0.
设M(x1,y1),N(x2,y2),线段MN的中点为Q(x3,y3),
则x1+x2=![]() .
.
所以x3=![]() =
=![]() ,y3=k(x3-1)=
,y3=k(x3-1)=![]() .
.
线段MN的垂直平分线的方程为
y+![]() =-
=-![]()
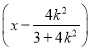 .
.
在上述方程中,令x=0,得y0=![]() =
=![]() .
.
当k<0时,![]() +4k≤-4
+4k≤-4![]() ;当k>0时,
;当k>0时,![]() +4k≥4
+4k≥4![]() .
.
所以-![]() ≤y0<0或0<y0≤
≤y0<0或0<y0≤![]() .
.
综上,y0的取值范围是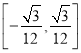 .
.


科目:高中数学 来源: 题型:
【题目】给出以下命题,
①命题“若![]() ,则
,则![]() 或
或![]() ”为真命题;
”为真命题;
②命题“若![]() ,则
,则![]() ”的否命题为真命题;
”的否命题为真命题;
③若平面![]() 上不共线的三个点到平面
上不共线的三个点到平面![]() 距离相等,则
距离相等,则![]()
④若![]() ,
,![]() 是两个不重合的平面,直线
是两个不重合的平面,直线![]() ,命题
,命题![]() ,命题
,命题![]() ,则
,则![]() 是
是![]() 的必要不充分条件;
的必要不充分条件;
⑤平面![]() 过正方体
过正方体![]() 的三个顶点
的三个顶点![]() ,且
,且![]() 与底面
与底面![]() 的交线为
的交线为![]() ,则
,则![]() ∥
∥![]() ;
;
其中,真命题的序号是______
查看答案和解析>>
科目:高中数学 来源: 题型:
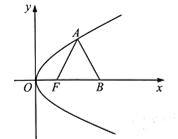
【题目】在平面直角坐标系![]() 中,已知点F为抛物线
中,已知点F为抛物线![]() 的焦点,点A在抛物线E上,
的焦点,点A在抛物线E上,
点B在x轴上,且![]() 是边长为2的等边三角形。
是边长为2的等边三角形。
(1)求抛物线E的方程;
(2)设C是抛物线E上的动点,直线![]() 为抛物线E在点C处的切线,求点B到直线
为抛物线E在点C处的切线,求点B到直线![]() 距离的最小值,并求此时点C的坐标。
距离的最小值,并求此时点C的坐标。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场对顾客实行购物优惠活动,规定 :一次购物总额
1)如果不超过500元,那么不予优惠;
2)如果超过500元但不超过1000元,那么超过500元部分按标价给予8折优惠;
3)如果超过1000元,那么其中超过500不超过1000元给予8折优惠,超过1000元部分给予5折优惠.设一次购物标价总额为x元,优惠后实际付款额为f(x)元.
(1)试写出f(x)的解析式;
(2)如果某顾客实际付款额为1600元,在这次优惠活动中他实际付款额比购物标价总额少支出多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过点A(0,1)且斜率为k的直线l与圆C:(x-2)2+(y-3)2=1交于M,N两点.
(1)求k的取值范围;
(2)若![]() =12,其中O为坐标原点,求|MN|.
=12,其中O为坐标原点,求|MN|.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于圆周率![]() ,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计
,数学发展史上出现过许多很有创意的求法,如著名的蒲丰实验和查理斯实验.受其启发,我们也可以通过设计下面的实验来估计![]() 的值:先请
的值:先请![]() 名同学,每人随机写下一个都小于1的正实数对
名同学,每人随机写下一个都小于1的正实数对![]() ;再统计两数能与1构成钝角三角形三边的数对
;再统计两数能与1构成钝角三角形三边的数对![]() 的个数
的个数![]() ;最后再根据统计数
;最后再根据统计数![]() 来估计
来估计![]() 的值.假如统计结果是
的值.假如统计结果是![]() ,那么可以估计
,那么可以估计![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com