
【题目】已知圆M:(x﹣1)2+y2= ![]() ,椭圆C:
,椭圆C: ![]() +y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
+y2=1,若直线l与椭圆交于A,B两点,与圆M相切于点P,且P为AB的中点,则这样的直线l有( )
A.2条
B.3条
C.4条
D.6条
 互动英语系列答案
互动英语系列答案科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)在定义域[-1,1]上既是奇函数,又是减函数.
(1)求证:对任意x1,x2∈[-1,1],有[f(x1)+f(x2)]·(x1+x2)≤0;
(2)若f(1-a)+f(1-a2)<0,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的可导函数f(x)满足f(x)﹣f(﹣x)=2x3 , 当x∈(﹣∞,0]时f'(x)<3x2 , 实数a满足f(1﹣a)﹣f(a)≥﹣2a3+3a2﹣3a+1,则a的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a∈R,函数f(x)满足f(2x)=x2﹣2ax+a2﹣1.
(Ⅰ)求f(x)的解析式,并写出f(x)的定义域;
(Ⅱ)若f(x)在 ![]() 上的值域为[﹣1,0],求实数a的取值范围.
上的值域为[﹣1,0],求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知椭圆C: ![]() +
+ ![]() =1(a>b>0)的左、右焦点分别为F1、F2 , 焦距为2,过点F2作直线l交椭圆于M、N两点,△F1MN的周长为8.
=1(a>b>0)的左、右焦点分别为F1、F2 , 焦距为2,过点F2作直线l交椭圆于M、N两点,△F1MN的周长为8. 
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l分别交直线y= ![]() x,y=﹣
x,y=﹣ ![]() x于P,Q两点,求
x于P,Q两点,求 ![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,∠ABC= ![]() ,边BC在平面α内,顶点A在平面α外,直线AB与平面α所成角为θ.若平面ABC与平面α所成的二面角为
,边BC在平面α内,顶点A在平面α外,直线AB与平面α所成角为θ.若平面ABC与平面α所成的二面角为 ![]() ,则sinθ= .
,则sinθ= . 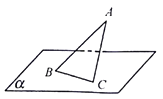
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊人常用小石子在沙滩上摆成各种形状来研究数.比如:他们研究过图(1)中的1,3,6,10,…,由于这些数能够表示成三角形,所以将其称为三角形数;类似地,称图(2)中的1,4,9,16,…这样的数为正方形数.下列数中既是三角形数又是正方形数的是( )


A. 289 B. 1 024
C. 1 225 D. 1 378
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个袋子里装有7个球,其中有红球4个,编号分别为1,2,3,4;白球3个,编号分别为2,3,4.从袋子中任取4个球(假设取到任何一个球的可能性相同).
(Ⅰ)求取出的4个球中,含有编号为3的球的概率;
(Ⅱ)在取出的4个球中,红球编号的最大值设为X,求随机变量X的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com