
【题目】已知函数f(x)=xlnx,
(1)求函数f(x)过(﹣1,﹣2)的切线的方程
(2)过点P(1,t)存在两条直线与曲线y=f(x)相切,求t的取值范围
【答案】(1)y=x﹣1(2)(﹣∞,0)
【解析】
(1)求导得到f′(x)=1+lnx,设切点为(m,n),利用切线方程公式计算得到答案.
(2)导数为f′(x)=1+lnx,设切点为(u,v)化简得到t﹣1=lnu﹣u在(0,+∞)有两解,求函数的最值得到答案.
(1)函数f(x)=xlnx的导数为f′(x)=1+lnx,
设切点为(m,n),可得切线的斜率为1+lnm,切线方程为y﹣mlnm=(1+lnm)(x﹣m),
代入(﹣1,﹣2),可得﹣2﹣mlnm=(1+lnm)(﹣1﹣m),
化为m+lnm=1,由y=x+lnx在(0,+∞)递增,且x=1时,y=1,
可得m+lnm=1的解为m=1,
则所求切线的方程为y=x﹣1;
(2)函数f(x)=xlnx的导数为f′(x)=1+lnx,
设切点为(u,v),则切线的斜率为f′(u)=1+lnu,
即有切线的方程为y﹣ulnu=(1+lnu)(x﹣u),
代入点P(1,t),即有t﹣ulnu=(1+lnu)(1﹣u),
即为t﹣1=lnu﹣u在(0,+∞)有两解,
由g(x)=lnx﹣x的导数为g′(x)![]() 1,
1,
可得x>1,g(x)递减,0<x<1,g(x)递增.
可得x=1,取得最大值g(1)=﹣1,即有t﹣1<﹣1,解得t<0.
故实数t的取值范围时(﹣∞,0).


科目:高中数学 来源: 题型:
【题目】已知曲线![]() 的方程为
的方程为![]() ,
,![]() 的方程为
的方程为![]() ,
,![]() 是一条经过原点且斜率大于
是一条经过原点且斜率大于![]() 的直线.
的直线.
(1)以直角坐标系原点![]() 为极点,
为极点,![]() 轴正方向为极轴建立极坐标系,求
轴正方向为极轴建立极坐标系,求![]() 与
与![]() 的极坐标方程;
的极坐标方程;
(2)若![]() 与
与![]() 的一个公共点
的一个公共点![]() (异于点
(异于点![]() ),
),![]() 与
与![]() 的一个公共点为
的一个公共点为![]() ,当
,当![]() 时,求
时,求![]() 的直角坐标方程.
的直角坐标方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求函数
,求函数![]() 的解析式;
的解析式;
(2)在(1)的条件下,若![]() 是函数
是函数![]() 的零点,且
的零点,且![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,函数
时,函数![]() 有两个零点
有两个零点![]() ,且
,且![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 三个内角
三个内角![]() 所对的边分别是
所对的边分别是![]() ,若
,若![]() .
.
(1)求角![]() ;
;
(2)若![]() 的外接圆半径为2,求
的外接圆半径为2,求![]() 周长的最大值.
周长的最大值.
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)由正弦定理将边角关系化为边的关系![]() ,再根据余弦定理求角
,再根据余弦定理求角![]() ,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
,(2)先根据正弦定理求边,用角表示周长,根据两角和正弦公式以及配角公式化为基本三角函数,最后根据正弦函数性质求最大值.
试题解析:(1)由正弦定理得![]() ,
,
∴![]() ,∴
,∴![]() ,即
,即![]()
因为![]() ,则
,则![]() .
.
(2)由正弦定理![]()
∴![]() ,
, ![]() ,
, ![]() ,
,
∴周长![]()
![]()
![]()
![]()
![]()
![]()
∵![]() ,∴
,∴![]()
∴当![]() 即
即![]() 时
时![]()
∴当![]() 时,
时, ![]() 周长的最大值为
周长的最大值为![]() .
.
【题型】解答题
【结束】
18
【题目】经调查,3个成年人中就有一个高血压,那么什么是高血压?血压多少是正常的?经国际卫生组织对大量不同年龄的人群进行血压调查,得出随年龄变化,收缩压的正常值变化情况如下表:

其中:  ,
, ![]() ,
, ![]()

(1)请画出上表数据的散点图;
(2)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;(
;(![]() 的值精确到0.01)
的值精确到0.01)
(3)若规定,一个人的收缩压为标准值的0.9~1.06倍,则为血压正常人群;收缩压为标准值的1.06~1.12倍,则为轻度高血压人群;收缩压为标准值的1.12~1.20倍,则为中度高血压人群;收缩压为标准值的1.20倍及以上,则为高度高血压人群.一位收缩压为180mmHg的70岁的老人,属于哪类人群?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年1月3日嫦娥四号探测器成功实现人类历史上首次月球背面软着陆,我国航天事业取得又一重大成就,实现月球背面软着陆需要解决的一个关键技术问题是地面与探测器的通讯联系.为解决这个问题,发射了嫦娥四号中继星“鹊桥”,鹊桥沿着围绕地月拉格朗日![]() 点的轨道运行.
点的轨道运行.![]() 点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,
点是平衡点,位于地月连线的延长线上.设地球质量为M1,月球质量为M2,地月距离为R,![]() 点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
点到月球的距离为r,根据牛顿运动定律和万有引力定律,r满足方程:
![]() .
.
设![]() ,由于
,由于![]() 的值很小,因此在近似计算中
的值很小,因此在近似计算中![]() ,则r的近似值为
,则r的近似值为
A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店,为合理安排各地区加盟店的个数,先在其中5个地区试点,得到试点地区加盟店个数分别为1,2,3,4,5时,单店日平均营业额![]() (万元)的数据如下:
(万元)的数据如下:
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
(1)求单店日平均营业额![]() (万元)与所在地区加盟店个数
(万元)与所在地区加盟店个数![]() (个)的线性回归方程;
(个)的线性回归方程;
(2)根据试点调研结果,为保证规模和效益,在其他5个地区,该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元,求一个地区开设加盟店个数![]() 的所有可能取值;
的所有可能取值;
(3)小赵与小王都准备加入该公司的加盟店,根据公司规定,他们只能分别从其他五个地区(加盟店都不少于2个)中随机选一个地区加入,求他们选取的地区相同的概率.
(参考数据及公式:![]() ,
,![]() ,线性回归方程
,线性回归方程![]() ,其中
,其中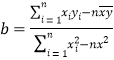 ,
,![]() .)
.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若定义在R上的函数![]() ,其图像是连续不断的,且存在常数
,其图像是连续不断的,且存在常数![]() 使得
使得![]() 对任意实数x都成立,则称
对任意实数x都成立,则称![]() 是一个“k~特征函数”.则下列结论中正确命题序号为____________.
是一个“k~特征函数”.则下列结论中正确命题序号为____________.
①![]() 是一个“k~特征函数”;②
是一个“k~特征函数”;②![]() 不是“k~特征函数”;
不是“k~特征函数”;
③![]() 是常数函数中唯一的“k~特征函数”;④“
是常数函数中唯一的“k~特征函数”;④“![]() ~特征函数”至少有一个零点;
~特征函数”至少有一个零点;
查看答案和解析>>
科目:高中数学 来源: 题型:
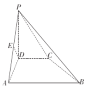
【题目】如下图,在四棱锥![]() 中,
中,![]() 面
面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点。
的中点。
(1)求证:![]() 面
面![]() ;
;
(2)线段![]() 上是否存在一点
上是否存在一点![]() ,满足
,满足![]() ?若存在,试求出二面角
?若存在,试求出二面角![]() 的余弦值;若不存在,说明理由。
的余弦值;若不存在,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com