
【题目】设![]() 是奇函数,
是奇函数,![]() 是偶函数
是偶函数![]() ,且其中
,且其中![]() .
.
(1)求![]() 和
和![]() 的表达式,并求函数
的表达式,并求函数![]() 的值域
的值域
(2)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 内恰有两个不等实根,求常数
内恰有两个不等实根,求常数![]() 的取值范围
的取值范围
【答案】(1)![]() 值域为
值域为![]() (2)
(2)![]()
【解析】
(1)由函数的奇偶性可得![]() ,再结合条件列方程组求解,进而可得
,再结合条件列方程组求解,进而可得![]() ,利用函数单调性可求得值域;
,利用函数单调性可求得值域;
(2)由题意得方程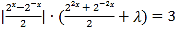 在区间
在区间![]() 内恰有两个不等实根,令
内恰有两个不等实根,令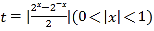 ,则可将方程转化为
,则可将方程转化为![]() 在区间
在区间![]() 内有唯一实根,利用函数单调性求得函数
内有唯一实根,利用函数单调性求得函数![]() 的值域,进而可得常数
的值域,进而可得常数![]() 的取值范围.
的取值范围.
(1)由已知![]() ①,
①,
以![]() 代
代![]() ,得
,得![]() ,
,
因为![]() 是奇函数,
是奇函数,![]() 是偶函数,
是偶函数,
所以![]() ②,
②,
联立①②可得![]() ,
,
![]() ,
,
又![]() ,
,![]() ,
,![]() ,于是
,于是![]() ,
,
![]() 函数
函数![]() 的值域为
的值域为![]() ;
;
(2)题意即方程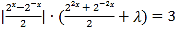 在区间
在区间![]() 内恰有两个不等实根.
内恰有两个不等实根.
显然![]() 不是该方程的根,所以令
不是该方程的根,所以令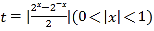
由![]() 得
得![]() ,则原方程可变形为
,则原方程可变形为![]()
易知函数![]() 为偶函数,且在区间
为偶函数,且在区间![]() 内单调递增,所以
内单调递增,所以![]()
且题意转化为方程![]() 在区间
在区间![]() 内有唯一实根(因为每一个
内有唯一实根(因为每一个![]() 在区间
在区间![]() 内恰有两个
内恰有两个![]() 值与之对应).
值与之对应).
易知![]() 在区间
在区间![]() 内单调递减,
内单调递减,
又![]() 时,
时,![]() ,
,
所以![]() (此时每一个
(此时每一个![]() ,在区间
,在区间![]() 内有且仅有一个
内有且仅有一个![]() 值与之对应).
值与之对应).
综上所述,所求常数![]() 的取值范围是
的取值范围是![]() .
.


科目:高中数学 来源: 题型:
【题目】如图所示的几何体是由以等边三角形![]() 为底面的棱柱被平面
为底面的棱柱被平面![]() 所截而得,已知
所截而得,已知![]() 平面
平面![]()
![]()
![]()
![]() 为
为![]() 的中点,
的中点, ![]() 面
面![]() .
.
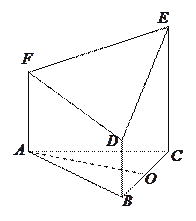
(1)求![]() 的长;
的长;
(2)求证:面![]() 面
面![]() ;
;
(3)求平面![]() 与平面
与平面![]() 相交所成锐角二面角的余弦值.
相交所成锐角二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(题文)已知等差数列{an}的首项a1≠0,前n项和为Sn,且S4+a2=2S3;等比数列{bn}满足b1=a2,b2=a4.
(1)求证:数列{bn}中的每一项都是数列{an}中的项;
(2)若a1=2,设cn=![]() ,求数列{cn}的前n项和Tn;
,求数列{cn}的前n项和Tn;
(3)在(2)的条件下,若有f(n)=log3Tn,求f(1)+f(2)+…+f(n)的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地区积极发展电商,通过近些年工作的开展在新农村建设和扶贫过程中起到了非常重要的作用,促进了农民生活富裕,为了更好地了解本地区某一特色产品的宣传费![]() (千元)对销量
(千元)对销量![]() (千件)的影响,统计了近六年的数据如下:
(千件)的影响,统计了近六年的数据如下:

(1)若近6年的宣传费![]() 与销量
与销量![]() 呈线性分布,由前5年数据求线性回归直线方程,并写出
呈线性分布,由前5年数据求线性回归直线方程,并写出![]() 的预测值;
的预测值;
(2)若利润与宣传费的比值不低于20的年份称为“吉祥年”,在这6个年份中任意选2个年份,求这2个年份均为“吉祥年”的概率
附:回归方程![]() 的斜率与截距的最小二乘法估计分别为
的斜率与截距的最小二乘法估计分别为 ,
,
![]() ,其中
,其中![]() ,
, ![]() 为
为![]() ,
, ![]() 的平均数.
的平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】科学研究表明:人类对声音有不的感觉,这与声音的强度![]() 单位:瓦
单位:瓦![]() 平方米
平方米![]() 有关
有关![]() 在实际测量时,常用
在实际测量时,常用![]() 单位:分贝
单位:分贝![]() 来表示声音强弱的等级,它与声音的强度I满足关系式:
来表示声音强弱的等级,它与声音的强度I满足关系式:![]() 是常数
是常数![]() ,其中
,其中![]() 瓦
瓦![]() 平方米
平方米![]() 如风吹落叶沙沙声的强度
如风吹落叶沙沙声的强度![]() 瓦
瓦![]() 平方米,它的强弱等级
平方米,它的强弱等级![]() 分贝.
分贝.
![]() 已知生活中几种声音的强度如表:
已知生活中几种声音的强度如表:
声音来源
声音大小 | 风吹落叶沙沙声 | 轻声耳语 | 很嘈杂的马路 |
强度 |
|
|
|
强弱等级 | 10 | m | 90 |
求a和m的值
![]() 为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
为了不影响正常的休息和睡眠,声音的强弱等级一般不能超过50分贝,求此时声音强度I的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() 的图象两相邻对称轴之间的距离是
的图象两相邻对称轴之间的距离是![]() ,若将
,若将![]() 的图象向右平移
的图象向右平移![]() 个单位长度,所得图象对应的函数
个单位长度,所得图象对应的函数![]() 为奇函数.
为奇函数.
(1)求![]() 的解析式;
的解析式;
(2)求![]() 的对称轴及单调增区间;
的对称轴及单调增区间;
(3)若对任意![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() ,(
,(![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系,曲线
轴的非负半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 的极坐标方程及曲线
的极坐标方程及曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)已知曲线![]() 交于
交于![]() 两点,过
两点,过![]() 点且垂直于
点且垂直于![]() 的直线与曲线
的直线与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com