
【题目】已知函数![]()
(1)![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 和
和![]() 的值;
的值;
(2)对任意的![]() ,
,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:
【题目】在新高考改革中,打破了文理分科的“![]() ”模式,不少省份采用了“
”模式,不少省份采用了“![]() ”,“
”,“![]() ”,“
”,“![]() ”等模式.其中“
”等模式.其中“![]() ”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
”模式的操作又更受欢迎,即语数外三门为必考科目,然后在物理和历史中选考一门,最后从剩余的四门中选考两门.某校为了了解学生的选科情况,从高二年级的2000名学生(其中男生1100人,女生900人)中,采用分层抽样的方法从中抽取n名学生进行调查.
(1)已知抽取的n名学生中含男生110人,求n的值及抽取到的女生人数;
(2)在(1)的情况下对抽取到的n名同学“选物理”和“选历史”进行问卷调查,得到下列2×2列联表.请将列联表补充完整,并判断是否有99%的把握认为选科目与性别有关?
选物理 | 选历史 | 合计 | |
男生 | 90 | ||
女生 | 30 | ||
合计 |
(3)在(2)的条件下,从抽取的“选历史”的学生中按性别分层抽样再抽取5名,再从这5名学生中抽取2人了解选政治、地理、化学、生物的情况,求2人至少有1名男生的概率.
参考公式: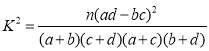 .
.
| 0.10 | 0.010 | 0.001 |
| 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax+x2,g(x)=xlna,a>1.
(1)求证:函数F(x)=f(x)-g(x)在(0,+∞)上单调递增;
(2)若函数y=![]() -3有四个零点,求b的取值范围;
-3有四个零点,求b的取值范围;
(3)若对于任意的x1,x2∈[-1,1]时,都有|F(x2)-F(x1)|≤e2-2恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 在区间
在区间![]() 上,
上, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 均可为一个三角形的三边长,则称函数
均可为一个三角形的三边长,则称函数![]() 为“三角形函数”.已知函数
为“三角形函数”.已知函数![]() 在区间
在区间![]() 上是“三角形函数”,则实数
上是“三角形函数”,则实数![]() 的取值范围为( )
的取值范围为( )
A.  B.
B. ![]()
C. ![]() D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)![]() 与g(x)=3elnx+mx的图象有4个不同的交点,则实数m的取值范围是( )
与g(x)=3elnx+mx的图象有4个不同的交点,则实数m的取值范围是( )
A.(﹣3,![]() )B.(﹣1,
)B.(﹣1,![]() )C.(﹣1,3)D.(0,3)
)C.(﹣1,3)D.(0,3)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com