解:(Ⅰ)因为锐角△ABC中,A+B+C=π,sinA=

,所以cosA=

,(2分)
则
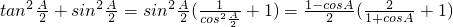
=
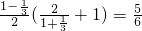
;(6分)
(Ⅱ)∵S
△ABC=

bcsinA=

bc•

=
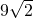
,则bc=27.(8分)
又a=6,cosA=

,由余弦定理:a
2=b
2+c
2-2bccosA得:b
2+c
2=54,
所以(b-c)
2=b
2+c
2-2bc=54-2×27=0,即b=c,
所以△ABC为等腰三角形.(12分)
分析:(Ⅰ)根据角A为锐角,由sinA的值,利用同角三角函数间的基本关系求出cosA的值,然后利用同角三角函数间的基本关系化简后提取sin
2
,利用二倍角的余弦函数公式化为关于cosA的式子,将求出的cosA的值代入即可求出值;
(Ⅱ)由三角形的面积公式表示出S
△ABC,让其值等于已知值,把sinA的值代入求出bc的值,利用余弦定理表示出a
2,将a与cosA的值代入求出b与c的平方和,利用差的完全平方公式化简(b-c)
2,将求出的b与c的平方和与bc的值代入即可求出值为0,进而得到b与c相等,故△ABC为等腰三角形.
点评:此题综合考查了同角三角函数间的基本关系,二倍角的余弦函数公式,余弦定理及三角形的面积公式.本题确定三角形形状的技巧性比较强,方法是:先利用三角形的面积公式求出bc的值,然后利用余弦定理求出b与c的平方和,借助差的完全平方公式得到b=c,从而得到三角形为等腰三角形.

 ,
,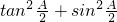 的值;
的值;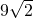 ,求证:△ABC为等腰三角形.
,求证:△ABC为等腰三角形. ,所以cosA=
,所以cosA= ,(2分)
,(2分)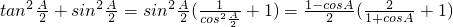
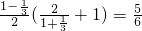 ;(6分)
;(6分) bcsinA=
bcsinA= bc•
bc• =
=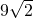 ,则bc=27.(8分)
,则bc=27.(8分) ,由余弦定理:a2=b2+c2-2bccosA得:b2+c2=54,
,由余弦定理:a2=b2+c2-2bccosA得:b2+c2=54, ,利用二倍角的余弦函数公式化为关于cosA的式子,将求出的cosA的值代入即可求出值;
,利用二倍角的余弦函数公式化为关于cosA的式子,将求出的cosA的值代入即可求出值;
