
【题目】某高校共有学生15000人,其中男生10500人,女生4500人.为调查该校学生每周平均体育运动时间的情况,采用分层抽样的方法,收集200位学生每周平均体育运动时间的样本数据(单位:小时).
(1)应收集多少位女生的样本数据?
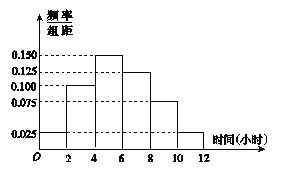
(2)根据这200个样本数据,得到学生每周平均体育运动时间的频率分布直方图,其中样本数据的分组区间为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .估计该校学生每周平均体育运动时间超过4小时的概率.
.估计该校学生每周平均体育运动时间超过4小时的概率.
(3)在样本数据中,有40位女生的每周平均体育运动时间超过4小时,请完成每周平均体育运动时间与性别列联表,并判断是否有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.(把表简要画在答题卡上)
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | |||
每周平均体育运动时间超过4小时 | |||
总计 |
附:
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.879 |
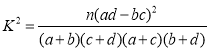
【答案】(1)60位(2)0.75.(3)见解析,没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.
【解析】
(1)由样本容量、频率和频数的关系求得应收集女生的样本数据;
(2)由频率分布直方图求得对应的概率值;
(3)由题意填写列联表,计算观测值,对照临界值得出结论.
(1)![]() ,所以应收集60位女生的样本数据.
,所以应收集60位女生的样本数据.
(2)由频率分布直方图得每周平均体育运动超过4小时的频率为![]() ,
,
所以该校学生每周平均体育运动时间超过4小时的概率的估计值为0.75.
(3)由(2)知,200位学生中有![]() (位)的每周平均体育运动时间超过4小时,50人的每周平均体育运动时间不超过4小时.又因为样本数据中有140份是关于男生的,60份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
(位)的每周平均体育运动时间超过4小时,50人的每周平均体育运动时间不超过4小时.又因为样本数据中有140份是关于男生的,60份是关于女生的,所以每周平均体育运动时间与性别列联表如下:
男生 | 女生 | 总计 | |
每周平均体育运动时间不超过4小时 | 30 | 20 | 50 |
每周平均体育运动时间超过4小时 | 110 | 40 | 150 |
总计 | 140 | 60 | 200 |
结合列联表可算得:![]()
所以,没有95%的把握认为“该校学生的每周平均体育运动时间与性别有关”.


科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,圆
中,圆![]() 的参数方程
的参数方程![]() (
(![]() 为参数).以
为参数).以![]() 为极点,
为极点,![]() 轴的非负半轴为极轴建立极坐标系.
轴的非负半轴为极轴建立极坐标系.
(1)求圆![]() 的极坐标方程;
的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆
与圆![]() 的交点为
的交点为![]() ,
,![]() ,与直线
,与直线![]() 的交点为
的交点为![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】改革开放四十年以来,北京市居民生活发生了翻天覆地的变化.随着经济快速增长、居民收入稳步提升,消费结构逐步优化升级,生活品质显著增强,美好生活蓝图正在快速构建.北京市城镇居民人均消费支出从1998年的7 500元增长到2017年的40 000元.1998年与2017年北京市城镇居民消费结构对比如下图所示:
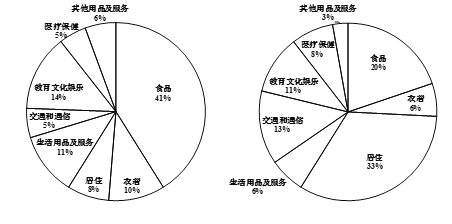
1998年北京市城镇居民消费结构 2017年北京市城镇居民消费结构
则下列叙述中不正确的是( )
A. 2017年北京市城镇居民食品支出占比同1998年相比大幅度降低
B. 2017年北京市城镇居民人均教育文化娱乐类支出同1998年相比有所减少
C. 2017年北京市城镇居民医疗保健支出占比同1998年相比提高约![]()
D. 2017年北京市城镇居民人均交通和通信类支出突破5 000元,大约是1998年的14倍
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为节能环保,推进新能源汽车推广和应用,对购买纯电动汽车的用户进行财政补贴. 某地补贴政策如下(![]() 表示纯电续航里程):
表示纯电续航里程):
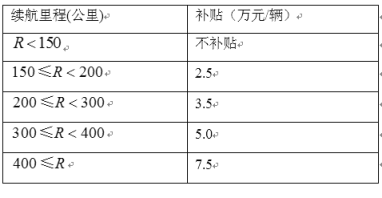
有![]() 三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)
三个纯电动汽车4s店分别销售不同品牌的纯电动汽车,在一个月内它们的销售情况如下: (每位客户只能购买一辆纯电动汽车)

(Ⅰ)从上述购买纯电动汽车的客户中随机选一人,求此人购买的是![]() 店纯电动汽车且享受补贴不低于3.5万元的概率;
店纯电动汽车且享受补贴不低于3.5万元的概率;
(Ⅱ)从购买![]() 店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
店纯电动汽车的客户中按分层抽样的方法随机选6人,再从这6人中随机选2人,进行使用满意度的调查,求这两人享受补贴恰好相同的概率;
(Ⅲ)分别用![]() 表示购买
表示购买![]() 店和
店和![]() 店纯电动汽车客户享受补贴的平均值,比较
店纯电动汽车客户享受补贴的平均值,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某渔船在航行中不幸遇险,发出求救信号,我海军舰艇在A处获悉后,立即测出该渔船在方位角为45°、距离A为10海里的C处,并测得渔船正沿方位角105°的方向,以9海里/时的速度向某小岛B靠拢,我海军舰艇立即以21海里/时的速度前去营救,恰在小岛B处追上渔船.
(1)试问舰艇应按照怎样的航向前进?
(2)求出舰艇靠近渔船所用的时间?
(参考数据:![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业生产一种产品,根据经验,其次品率Q与日产量x(万件)之间满足关系,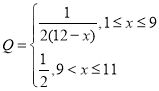 ,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如
,已知每生产1万件合格的产品盈利2万元,但每生产1万件次品将亏损1万元(注:次品率=次品数/生产量, 如![]() 表示每生产10件产品,有1件次品,其余为合格品).
表示每生产10件产品,有1件次品,其余为合格品).
(1)试将生产这种产品每天的盈利额![]() (万元)表示为日产量x(万件)的函数;
(万元)表示为日产量x(万件)的函数;
(2)当日产量为多少时,可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】研究变量![]() 得到一组样本数据,进行回归分析,有以下结论
得到一组样本数据,进行回归分析,有以下结论
①残差图中残差点所在的水平带状区域越窄,则回归方程的预报精确度越高;
②用相关指数![]() 来刻画回归效果,
来刻画回归效果,![]() 越小说明拟合效果越好;
越小说明拟合效果越好;
③在回归直线方程![]() 中,当变量
中,当变量![]() 每增加1个单位时,变量
每增加1个单位时,变量![]() 就增加2个单位
就增加2个单位
④若变量![]() 和
和![]() 之间的相关系数为
之间的相关系数为![]() ,则变量
,则变量![]() 和
和![]() 之间的负相关很强
之间的负相关很强
以上正确说法的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】生男生女都一样,女儿也是传后人.由于某些地区仍然存在封建传统思想,头胎的男女情况可能会影响生二孩的意愿,现随机抽取某地200户家庭进行调查统计.这200户家庭中,头胎为女孩的频率为0.5,生二孩的频率为0.525,其中头胎生女孩且生二孩的家庭数为60.
(1)完成下列![]() 列联表:
列联表:
生二孩 | 不生二孩 | 合计 | |
头胎为女孩 | 60 | ||
头胎为男孩 | |||
合计 | 200 |
(2)判断能否有![]() 的把握认为是否生二孩与头胎的男女情况有关;附:
的把握认为是否生二孩与头胎的男女情况有关;附:
| 0,15 | 0.05 | 0.01 | 0.0012.0 |
k | 2.072 | 3.841 | 6.635 | 10.828 |
 (其中
(其中![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com