练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】一个正三棱柱的三视图如图所示，若该三棱柱的外接球的表面积为，则侧视图中的的值为 （ ）

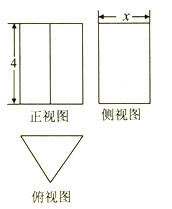
    A. 6 B. 4 C. 3 D. 2

    【答案】C

    【解析】分析：首先通过观察几何体的三视图，还原几何体，得知其为一个正三棱柱，结合直三棱柱的外接球的球心在上下底面外心连线的中点处，利用外接球的表面积，得到底面边长所满足的关系式，求得其边长，再根据侧视图中对应的边长与底面边长的关系，求得结果.

    详解：根据题中所给的几何体的三视图，可以得到该几何体是一个正三棱柱，

    设其底面边长为，则底面正三角形的外接圆的半径为，

    设该三棱锥的外接球的半径为R，

    结合正三棱锥的外接球的球心在上下底面的外心连线的中点处，

    则有，因为该三棱柱的外接球的表面积为，

    则有，从而解得，

    因为侧视图中对应的边为底面三角形的边的中线，

    求得，故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】如图，由A，B两个元件分别组成串联电路（图（1））和并联电路（图（2）），观察两个元件正常或失效的情况.

    （1）写出试验的样本空间；

    （2）对串联电路，写出事件M=“电路是通路”包含的样本点；

    （3）对并联电路，写出事件N=“电路是断路”包含的样本点.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f(x)是定义在R上的偶函数，当时，，现已画出函数在y轴左侧的图象，如图所示，请根据图象.

    （1）将函数的图象补充完整，并写出函数的递增区间；

    （2）写出函数的解析式；

    （3）若函数，求函数的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】《九章算术》里有一段叙述：今有良马与驽马发长安至齐，齐去长安一千一百二十五里，良马初日行一百零三里，日增十三里；驽马初日行九十七里，日减半里；良马先至齐，复还迎驽马，二马相逢.根据该问题设计程序框图如下，若输入，则输出的值是（ ）

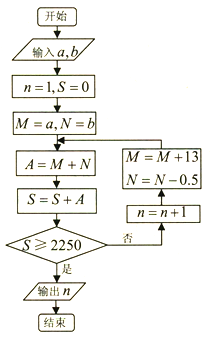
    A. 8 B. 9 C. 12 D. 16

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若曲线在点处的切线方程为，求的值；

    （2）当时，求证：；

    （3）设函数，其中为实常数，试讨论函数的零点个数，并证明你的结论．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】狄利克雷函数是高等数学中的一个典型函数，若，则称为狄利克雷函数．对于狄利克雷函数，给出下面4个命题：①对任意，都有；②对任意，都有；③对任意，都有， ；④对任意，都有．其中所有真命题的序号是（ ）

    A. ①④ B. ②③ C. ①②③ D. ①③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校20名同学的数学和英语成绩如下表所示：

    将这20名同学的两颗成绩绘制成散点图如图：

    根据该校以为的经验，数学成绩与英语成绩线性相关.已知这名学生的数学平均成绩为，英语平均成绩，考试结束后学校经过调查发现学号为的同学与学号为的同学（分别对应散点图中的）在英语考试中作弊，故将两位同学的两科成绩取消.

    取消两位作弊同学的两科成绩后，求其余同学的数学成绩与英语成绩的平均数；

    取消两位作弊同学的两科成绩后，求数学成绩x与英语成绩y的线性回归直线方程，并据此估计本次英语考试学号为8的同学如果没有作弊的英语成绩.（结果保留整数）

    附：位同学的两科成绩的参考数据：

    参考公式：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明同学在寒假社会实践活动中，对白天平均气温与某家奶茶店的品牌饮料销量之间的关系进行了分析研究，他分别记录了1月11日至1月15日的白天气温（）与该奶茶店的品牌饮料销量（杯），得到如表数据：

    日期

    1月11号

    1月12号

    1月13号

    1月14号

    1月15号

    平均气温（）

    9

    10

    12

    11

    8

    销量（杯）

    23

    25

    30

    26

    21

    （1）若先从这五组数据中抽出2组，求抽出的2组数据恰好是相邻2天数据的概率；

    （2）请根据所给五组数据，求出关于的线性回归方程式；

    （3）根据（2）所得的线性回归方程，若天气预报1月16号的白天平均气温为，请预测该奶茶店这种饮料的销量.

    （参考公式：，）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设圆的圆心为A，直线过点B（1,0）且与轴不重合，交圆A于C，D两点，过B作AC的平行线交AD于点E.

    （Ⅰ）证明：为定值，并写出点E的轨迹方程；

    （Ⅱ）设点E的轨迹为曲线C1，直线交C1于M,N两点，过B且与垂直的直线与C1交于P,Q两点， 求证：是定值，并求出该定值.

    查看答案和解析>>

    同步练习册答案