
【题目】解方程ln(2x+1)=ln(x2﹣2);
求函数f(x)=( ![]() )2x+2×(
)2x+2×( ![]() )x(x≤﹣1)的值域.
)x(x≤﹣1)的值域.
【答案】解:由题意:ln(2x+1)=ln(x2﹣2);
所以有 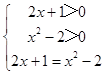 x=3 或﹣1(负舍)
x=3 或﹣1(负舍)
故方程的解为{x|x=3};
函数f(x)=( ![]() )2x+2×(
)2x+2×( ![]() )x(x≤﹣1)
)x(x≤﹣1)
令t= ![]() ∈[2,+∞),换元后得:
∈[2,+∞),换元后得:
g(t)=t2+2t (t≥2)
g(t)为一元二次函数,开口朝上,对称轴为t=﹣1,知:
g(t)在(2,+∞)上单调递增,g(t)min=8
故g(t)的值域为[8,+∞)
【解析】(1)根据方程式,方程的解需要满足函数定义域要求,再根据对数相等即可列出方程式;(2)利用换元法转化为一元二次函数来求原函数的值域即可;
【考点精析】认真审题,首先需要了解函数的值域(求函数值域的方法和求函数最值的常用方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的),还要掌握对数的运算性质(①加法:![]() ②减法:
②减法:![]() ③数乘:
③数乘:![]() ④
④![]() ⑤
⑤![]() )的相关知识才是答题的关键.
)的相关知识才是答题的关键.


科目:高中数学 来源: 题型:
【题目】为了展示中华汉字的无穷魅力,传递传统文化,提高学习热情,某校开展《中国汉字听写大会》的活动.为响应学校号召,2(9)班组建了兴趣班,根据甲、乙两人近期8次成绩画出茎叶图,如图所示(把频率当作概率).

(1)求甲、乙两人成绩的平均数和中位数;
(2)现要从甲、乙两人中选派一人参加比赛,从统计学的角度,你认为派哪位学生参加比较合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=log22x﹣mlog2x+2,其中m∈R.
(1)当m=3时,求方程f(x)=0的解;
(2)当x∈[1,2]时,求f(x)的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高一(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的污损,可见部分如图.

(Ⅰ)求分数在[50,60)的频率及全班人数;
(Ⅱ)求分数在[80,90)之间的频数,并计算频率分布直方图中[80,90)间矩形的高;
(Ⅲ)若要从分数在[80,100)之间的试卷中任取两份分析学生失分情况,求在抽取的试卷中,至少有一份分数在[90,100)之间的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 上的任一点到焦点的距离最大值为3,离心率为
上的任一点到焦点的距离最大值为3,离心率为![]() ,
,
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若![]() 为曲线
为曲线![]() 上两点,
上两点, ![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,求直线
,求直线![]() 被圆
被圆![]() 截得弦长的最大值及此时直线
截得弦长的最大值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() ,x∈R,a∈R.
,x∈R,a∈R.
(1)a=1时,求证:f(x)在区间(﹣∞,0)上为单调增函数;
(2)当方程f(x)=3有解时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高三共有800名学生,为了解学生3月月考生物测试情况,根据男女学生人数差异较大,从中随机抽取了200名学生,记录他们的分数,并整理得如图频率分布直方图.
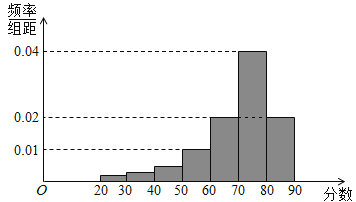
(1)若成绩不低于60分的为及格,成绩不低于80分的为优秀,试估计总体中合格的有多少人?优秀的有多少人?
(2)已知样本中有一半的女生分数不小于80,且样本中不低于80分的男女生人数之比2:3,试估计总体中男生和女生人数的比例.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com